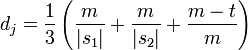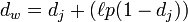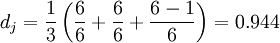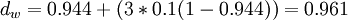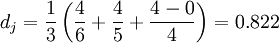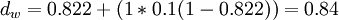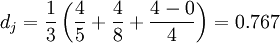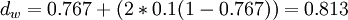Jaro-Winkler

Distance de Jaro-Winkler

La distance de Jaro-Winkler mesure la similarité entre deux chaînes de caractères. Il s'agit d'une variante proposée en 1999 par William E. Winkler, découlant de la distance de Jaro (1989, Matthew A. Jaro) qui est principalement utilisée dans la détection de doublons.

Plus la distance de Jaro-Winkler entre deux chaînes est élevée, plus elles sont similaires. Cette mesure est particulièrement adaptée au traitement de chaînes courtes comme des noms ou des mots de passe. Le résultat est normalisé de façon à avoir une mesure entre 0 et 1, le zéro représentant l'absence de similarité.

Distance de Jaro

La distance de Jaro entre chaînes $s 1$ et $s 2$ est définie par :

$d_j = \frac{1}{3}\left(\frac{m}{|s_1|} + \frac{m}{|s_2|} + \frac{m-t}{m}\right)$

où:

$m$ est le nombre de caractères correspondants (voir ci-dessous);
$t$ est le nombre de transpositions (voir ci-dessous).

Deux caractères identiques de $s 1$ et de $s 2$ sont considérés comme correspondants si leur éloignement (i.e. la différence entre leurs positions dans leurs chaînes respectives) ne dépasse pas :

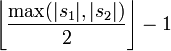$\left\lfloor\frac{\max(|s_1|,|s_2|)}{2}\right\rfloor-1$ .

Le nombre de transpositions est obtenu en comparant le i-ème caractère correspondant de $s 1$ avec le i-ème caractère correspondant de $s 2$ . Le nombre de fois où ces caractères sont différents, divisé par deux, donne le nombre de transpositions.

Distance de Jaro-Winkler

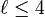La méthode introduite par Winkler utilise un coefficient de préfixe $p$ qui favorise les chaînes commençant par un préfixe de longueur $\ell$ (avec $\ell \le 4$ ). En considérant deux chaînes $s 1$ et $s 2$ , leur distance de Jaro-Winkler $d w$ est :

$d_w = d_j + (\ell p (1 - d_j))$

où :

$d j$ est la distance de Jaro entre $s 1$ et $s 2$
$\ell$ est la longueur du préfixe commun (maximum 4 caractères)
$p$ est un coefficient qui permet de favoriser les chaînes avec un préfixe commun. Winkler propose pour valeur $p = 0.1$

Exemples

Soit deux chaînes $s 1$ MARTHA et $s 2$ MARHTA. La table de correspondance est :

	M	A	R	T	H	A
M	1	0	0	0	0	0
A	0	1	0	0	0	0
R	0	0	1	0	0	0
H	0	0	0	0	1	0
T	0	0	0	1	0	0
A	0	0	0	0	0	1

$m = 6$ (nombre de 1 dans la table)
$| s 1 | = 6$
$| s 2 | = 6$
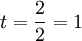
Les caractères correspondants sont {M,A,R,T,H,A} pour $s 1$ et {M,A,R,H,T,A} pour $s 2$ . En considérant ces ensembles ordonnés, on a donc 2 couples (T/H et H/T) de caractères correspondants différents, soit deux demi-transpositions. D'où $t = \frac{2}{2} = 1$

La distance de Jaro est :

$d_j = \frac{1}{3}\left(\frac{6}{6} + \frac{6}{6} + \frac{6-1}{6}\right) = 0.944$

La distance de Jaro-Winkler avec $p = 0.1$ avec un préfixe de longueur 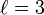$\ell=3$ devient

$d_w = 0.944 + (3 * 0.1 (1 - 0.944)) = 0.961~$

Avec les chaînes $s 1$ DWAYNE et $s 2$ DUANE on trouve :

$m = 4$
$| s 1 | = 6$
$| s 2 | = 5$
$t = 0$

La distance de Jaro est :

$d_j = \frac{1}{3}\left(\frac{4}{6} + \frac{4}{5} + \frac{4-0}{4}\right) = 0.822$

Celle de Jaro-Winkler avec $\ell = 1$ :

$d_w = 0.822 + (1 * 0.1 (1 - 0.822)) = 0.84~$

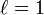Avec les chaînes $s 1$ DIXON et $s 2$ DICKSONX, on obtient :

	D	I	X	O	N
D	1	0	0	0	0
I	0	1	0	0	0
C	0	0	0	0	0
K	0	0	0	0	0
S	0	0	0	0	0
O	0	0	0	1	0
N	0	0	0	0	1
X	0	0	0	0	0

On calcule l'éloignement maximum pour le critère de correspondance

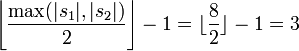$\left\lfloor\frac{\max(|s_1|,|s_2|)}{2}\right\rfloor-1 = \lfloor\frac{8}{2}\rfloor-1=3$ .

$m = 4$ (les deux X ne correspondent pas, car ils sont éloignés de plus de 3 caractères)
$| s 1 | = 5$
$| s 2 | = 8$
$t = 0$

La distance de Jaro :

$d_j = \frac{1}{3}\left(\frac{4}{5} + \frac{4}{8} + \frac{4-0}{4}\right) = 0.767$

La distance de Jaro-Winkler avec $\ell = 2$ :

$d_w = 0.767 + (2 * 0.1 (1 - 0.767)) = 0.813~$

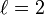Références

Jaro, M. A., « Advances in record linking methodology as applied to the 1985 census of Tampa Florida », dans Journal of the American Statistical Society, vol. 84, n^o 406, 1989, p. 414-420
Jaro, M. A., « Probabilistic linkage of large public health data file », dans Statistics in Medicine, vol. 14, 1995, p. 491-498 [texte intégral]
Winkler, W. E., « The state of record linkage and current research problems », dans Statistics of Income Division, Internal Revenue Service Publication R99/04, 1999 [texte intégral]
Winkler, W. E., « Overview of Record Linkage and Current Research Directions », dans Research Report Series, RRS, 2006 [texte intégral]

Liens externes

(en) Implémentation Opensource en Java et .NET
(en) Implémentation originale en C
(fr) Implémentation en Delphi
(fr) Implémentation simple en C

Algorithme de manipulation de texte
Algorithme de recherche de sous-chaîne	Algorithme d'Aho-Corasick - Algorithme de Boyer-Moore - Algorithme de Knuth-Morris-Pratt - Algorithme de Rabin-Karp
Algorithmes d'alignement de chaînes	Algorithme de Needleman-Wunsch
Algorithmes de mesure de similarité	Distance de Jaro-Winkler - Distance de Levenshtein - Distance de Hamming

Portail de l’informatique

Ce document provient de « Distance de Jaro-Winkler ».

Catégorie : Algorithme sur les chaînes de caractères

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Jaro-Winkler de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Jaro-Winkler distance — The Jaro Winkler distance (Winkler, 1999) is a measure of similarity between two strings. It is a variant of the Jaro distance metric (Jaro, 1989, 1995) and mainly used in the area of record linkage (duplicate detection). The higher the Jaro… … Wikipedia
Distance de Jaro-Winkler — La distance de Jaro Winkler mesure la similarité entre deux chaînes de caractères. Il s agit d une variante proposée en 1999 par William E. Winkler, découlant de la distance de Jaro (1989, Matthew A. Jaro) qui est principalement utilisée dans la… … Wikipédia en Français
Jaro — may refer to either of two places in the Philippines: *Jaro, Leyte a municipality in the province of Leyte *Jaro, Iloilo City a district of Iloilo Cityee also*Jaro Winkler distance *Jaro Medien (Jaro Media) a German music company * Jaro Records … Wikipedia
Distance de Jaro — Winkler La distance de Jaro Winkler mesure la similarité entre deux chaînes de caractères. Il s agit d une variante proposée en 1999 par William E. Winkler, découlant de la distance de Jaro (1989, Matthew A. Jaro) qui est principalement utilisée… … Wikipédia en Français
Algorithme de Levenshtein — Distance de Levenshtein La distance de Levenshtein mesure la similarité entre deux chaînes de caractères. Elle est égale au nombre minimal de caractères qu il faut supprimer, insérer ou remplacer pour passer d’une chaîne à l’autre. Son nom… … Wikipédia en Français
Distance De Levenshtein — La distance de Levenshtein mesure la similarité entre deux chaînes de caractères. Elle est égale au nombre minimal de caractères qu il faut supprimer, insérer ou remplacer pour passer d’une chaîne à l’autre. Son nom provient de Vladimir… … Wikipédia en Français
Distance de levenshtein — La distance de Levenshtein mesure la similarité entre deux chaînes de caractères. Elle est égale au nombre minimal de caractères qu il faut supprimer, insérer ou remplacer pour passer d’une chaîne à l’autre. Son nom provient de Vladimir… … Wikipédia en Français
String metric — String metrics (also known as similarity metrics) are a class of textual based metrics resulting in a similarity or dissimilarity (distance) score between two pairs of text strings for approximate matching or comparison and in fuzzy string… … Wikipedia
SimMetrics — is an open source extensible library of similarity or distance metrics (also known as string metrics). The SimMetrics open source library includes the following metrics * Levenshtein distance, * Block distance or city block distance or L2… … Wikipedia
Levenshtein distance — In information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences. The term edit distance is often used to refer specifically to Levenshtein distance. The… … Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Jaro-Winkler

Distance de Jaro-Winkler

Sommaire

Distance de Jaro

Distance de Jaro-Winkler

Exemples

Références

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Jaro-Winkler

Distance de Jaro-Winkler

Sommaire

Distance de Jaro

Distance de Jaro-Winkler

Exemples

Références

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link