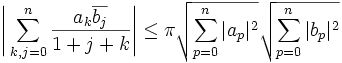Inégalité de hilbert
- Inégalité de hilbert
-
Inégalité de Hilbert
L' inégalité de Hilbert est un résultat découvert par le mathématicien allemand David Hilbert en 1905.
Si 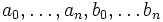 sont des nombres complexes, alors on a l'inégalité suivante :
sont des nombres complexes, alors on a l'inégalité suivante :
-
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inégalité de hilbert de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Inegalite de Hilbert — Inégalité de Hilbert L inégalité de Hilbert est un résultat découvert par le mathématicien allemand David Hilbert en 1905. Si sont des nombres complexes, alors on a l inégalité suivante … Wikipédia en Français
Inégalité De Hilbert — L inégalité de Hilbert est un résultat découvert par le mathématicien allemand David Hilbert en 1905. Si sont des nombres complexes, alors on a l inégalité suivante … Wikipédia en Français
Inégalité de Hilbert — L inégalité de Hilbert est un résultat découvert par le mathématicien allemand David Hilbert en 1905. Si sont des nombres complexes, alors on a l inégalité suivante … Wikipédia en Français
Hilbert — David Hilbert David Hilbert David Hilbert en 1912 Naissance 23 janvier 1862 Königsberg (Prusse Orientale) … Wikipédia en Français
HILBERT (ESPACE DE) — La théorie des espaces hilbertiens trouve son origine dans celle des développements de fonctions arbitraires en séries de fonctions orthogonales, lesquelles apparaissent le plus souvent comme fonctions propres de certains opérateurs différentiels … Encyclopédie Universelle
Inegalite de Bessel — Inégalité de Bessel En géométrie euclidienne ou hilbertienne, l inégalité de Bessel est un résultat étroitement lié à la question de la projection orthogonale. Elle tient son nom du mathématicien allemand Friedrich Wilhelm Bessel. Sommaire 1… … Wikipédia en Français
Inégalité De Bessel — En géométrie euclidienne ou hilbertienne, l inégalité de Bessel est un résultat étroitement lié à la question de la projection orthogonale. Elle tient son nom du mathématicien allemand Friedrich Wilhelm Bessel. Sommaire 1 Énoncé pour une famille… … Wikipédia en Français
Inégalité de bessel — En géométrie euclidienne ou hilbertienne, l inégalité de Bessel est un résultat étroitement lié à la question de la projection orthogonale. Elle tient son nom du mathématicien allemand Friedrich Wilhelm Bessel. Sommaire 1 Énoncé pour une famille… … Wikipédia en Français
Inegalite de Cauchy-Schwarz — Inégalité de Cauchy Schwarz Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de… … Wikipédia en Français
Inégalité De Cauchy-Schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
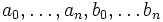 sont des nombres complexes, alors on a l'inégalité suivante :
sont des nombres complexes, alors on a l'inégalité suivante :