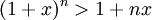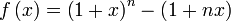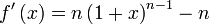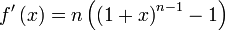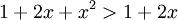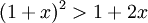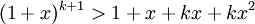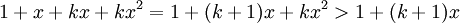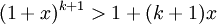Inegalite de Bernoulli

Inegalite de Bernoulli

Inégalité de Bernoulli

Définition

L'inégalité de Bernoulli stipule que :

(1+x)^n > 1+nx~

pour tout entier naturel n ≥ 2 et tout nombre réel x non nul et strictement supérieur à −1.

Démonstration

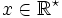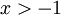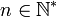Soitx\in\mathbb{R^{\star}} tel que x > -1~ et n\in\mathbb{N^*} et on cherche à montrer que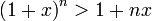 \left(1+x\right)^n > 1+nx

On va définir la fonction f définie sur \mathbb{R} par :

f\left(x\right)=\left(1+x\right)^n - \left(1+nx\right)

On va montrer que la fonction f(x) > 0 sur l'intervalle \left]-1,0\right[ \cup \left]0,+\infty\right[
La dérivée de la fonction sur le domaine considéré est :

f'\left(x\right)=n\left(1+x\right)^{n-1}-n
f'\left(x\right)=n\left(\left(1+x\right)^{n-1}-1\right)

On étudie maintenant le signe de la dérivée :

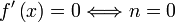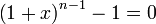
f'\left(x\right)=0 \Longleftrightarrow n=0 ou \left(1+x\right)^{n-1}-1 = 0

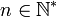or n\in\mathbb{N^*} donc:

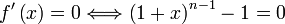
f'\left(x\right)=0 \Longleftrightarrow \left(1+x\right)^{n-1}-1 = 0
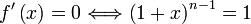
f'\left(x\right)=0 \Longleftrightarrow \left(1+x\right)^{n-1}=1
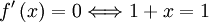f'\left(x\right)=0 \Longleftrightarrow 1+x = 1 ou n − 1 = 0
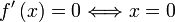f'\left(x\right)=0 \Longleftrightarrow x = 0 oun = 1
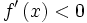f'\left(x\right)<0 pour x\in\left]-1,0\right[ et
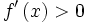f'\left(x\right)>0 pour x\in\left]0,+\infty\right[

La fonction f est donc strictement décroissante sur l'intervalle \left]-1,0\right[ et strictement croissante sur l'intervalle \left]0,+\infty\right[.
Pour x=0~, on a \left(1+x\right)^n - \left(1+nx\right)=0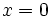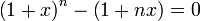
On a donc bien f > 0 sur l'intervalle \left]-1,0\right[ \cup \left]0,+\infty\right[.

Autre démonstration

Voici une démonstration par récurrence

1) Initialisation :

Pour n=2 en supposant x non nul on a :

1+2x+x^2>1+2x~

ou encore :

(1+x)^2>1+2x~

Donc la propriété est vraie au rang 2.

2) Hérédité :

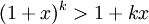
Hypothèse de récurrence : (1+x)^k>1+kx~

Montrons que la propriété est vraie au rang suivant k+1 :

(1+x)^k>1+kx~
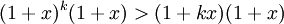(1+x)^k(1+x)>(1+kx)(1+x)~ en effet on ne change pas le sens de l'inégalité car on suppose x>-1 donc x+1>0
(1+x)^{k+1}>1+x+kx+kx^2~

Or

1+x+kx+kx^2=1+(k+1)x+kx^2>1+(k+1)x~

D'où

(1+x)^{k+1}>1+(k+1)x~

3) Conclusion :

La propriété est vraie au rang 2 et elle est héréditaire donc vraie pour tout entier n supérieur ou égal à 2 avec x non nul et strictement supérieur à -1.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « In%C3%A9galit%C3%A9 de Bernoulli ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Inegalite de Bernoulli de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Inégalité De Bernoulli — Définition L inégalité de Bernoulli stipule que : pour tout entier naturel n ≥ 2 et tout nombre réel x non nul et strictement supérieur à −1. Démonstration Soit tel que et …   Wikipédia en Français

  • Inégalité de bernoulli — Définition L inégalité de Bernoulli stipule que : pour tout entier naturel n ≥ 2 et tout nombre réel x non nul et strictement supérieur à −1. Démonstration Soit tel que et …   Wikipédia en Français

  • Inégalité de Bernoulli — Sommaire 1 Définition 2 Démonstration par récurrence 3 Généralisation 4 Notes et références …   Wikipédia en Français

  • inégalité de Bernoulli — Bernulio nelygybė statusas T sritis fizika atitikmenys: angl. Bernoulli’s inequality vok. Bernoullische Ungleichung, f rus. неравенство Бернулли, n pranc. inégalité de Bernoulli, f …   Fizikos terminų žodynas

  • Bernoulli — Famille Bernoulli Les Bernoulli qui se sont illustrés dans les mathématiques et la physique, sont issus de Nicolas Bernoulli (1623 1708), descendant d une famille ayant émigré d Anvers à Bâle à la fin du XVIe siècle. Les représentants les… …   Wikipédia en Français

  • Bernoulli’s inequality — Bernulio nelygybė statusas T sritis fizika atitikmenys: angl. Bernoulli’s inequality vok. Bernoullische Ungleichung, f rus. неравенство Бернулли, n pranc. inégalité de Bernoulli, f …   Fizikos terminų žodynas

  • Inégalité de Le Cam — L’inégalité de Le Cam[1], due à Lucien Le Cam, précise la rapidité de convergence de la loi de la somme d un grand nombre de variables de Bernoulli indépendantes de petit paramètre vers la loi de Poisson. Sa démonstration, élégante et peu… …   Wikipédia en Français

  • Inégalité FKG — L’inégalité FKG, due à Fortuin, Kasteleyn et Ginibre[1] est une version généralisée de l inégalité de Tchebychev pour les sommes. C est une inégalité de corrélation utilisée, par exemple, en théorie de la percolation, et dans l étude du modèle de …   Wikipédia en Français

  • Inégalité d'Azuma — L’inégalité d Azuma, parfois appelée inégalité d Azuma Hoeffding, est une inégalité de concentration concernant les martingales dont les accroissements sont bornés. C est une généralisation de l inégalité de Hoeffding, une inégalité de… …   Wikipédia en Français

  • Inégalité de Fano — L inégalité de Fano est un résultat de théorie de l information. Énoncé Pour deux variables aléatoires X et Y prenant r+1 valeurs possibles, on a : où Pe est la probabilité d erreur (ie. ) et H(Pe) est l entropie de Shannon de la loi de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”