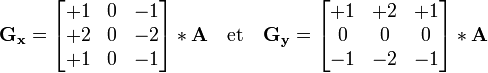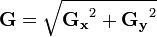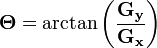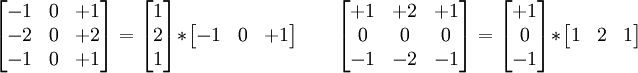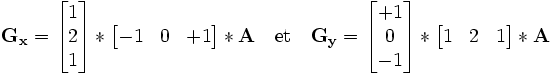Algorithme De Sobel

Exemple de détection de contours avec opérateurs Sobel, ici : G=abs(Gx)+abs(Gy).

L’algorithme de Sobel est un opérateur utilisé en traitement d'image pour la détection de contours. Il s'agit d'un des opérateurs les plus simples qui donne toutefois des résultats corrects.

Description simplifiée

Pour faire simple, l'opérateur calcule le gradient de l'intensité de chaque pixel. Ceci indique la direction de la plus forte variation du clair au sombre, ainsi que le taux de changement dans cette direction. On connaît alors les points de changement soudain de luminosité, correspondant probablement à des bords, ainsi que l'orientation de ces bords.

En termes mathématiques, le gradient d'une fonction de deux variables (ici l'intensité en fonction des coordonnées de l'image) est un vecteur de dimension 2 dont les coordonnées sont les dérivées selon les directions horizontale et verticale. En chaque point, le gradient pointe dans la direction du plus fort changement d'intensité, et sa longueur représente le taux de variation dans cette direction. Le gradient dans une zone d'intensité constante est donc nul. Au niveau d'un contour, le gradient traverse le contour, des intensités les plus sombres aux intensités les plus claires.

Formulation

L'opérateur utilise des matrices de convolution. La matrice (généralement de taille 3×3) subit une convolution avec l'image pour calculer des approximations des dérivées horizontale et verticale. Soit 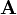l'image source, 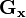et 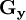deux images qui en chaque point contiennent des approximations respectivement de la dérivée horizontale et verticale de chaque point. Ces images sont calculées comme suit:

En chaque point, les approximations des gradients horizontaux et verticaux peuvent être combinées comme suit pour obtenir une approximation de la norme du gradient:

On peut également calculer la direction du gradient comme suit :

où, par exemple, 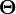vaut 0 pour un contour vertical plus foncé à gauche.

Précisions

Puisque l'intensité d'une image numérique est discrète, les dérivées de cette fonction ne peuvent pas être définies si ce n'est sous une hypothèse de continuité de la fonction intensité continue qui a été échantillonnée. En pratique on peut calculer des approximations plus ou moins fidèles du gradient en chaque point.

L'algorithme de Sobel calcule une approximation assez inexacte du gradient d'intensité, mais cela suffit en pratique dans beaucoup de cas. En effet, il n'utilise qu'un voisinage (généralement de taille 3×3) autour de chaque point pour calculer le gradient, et les poids utilisés pour le calcul du gradient sont entiers.

Détails d'implémentation

De par sa simplicité, l'algorithme de Sobel peut être aisément implémenté de manière logicielle ou même matérielle : seulement huit points autour du point considéré sont nécessaires pour calculer le gradient. Ce calcul utilise simplement des calculs sur les entiers. De plus, les filtres horizontal et vertical sont séparables :

et les deux dérivées 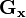et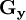 peuvent être calculées comme suit :

La séparabilité peut être mise à profit dans certains types d'implémentation pour permettre moins d'opérations lors du calcul.

Plus fondamentalement, en divisant par quatre, ces formules montrent que la dérivation dans une direction est associée à un lissage triangulaire dans l'autre direction destiné à éliminer les « faux contours », la même technique étant utilisée dans le filtre de Prewitt avec un lissage rectangulaire qui introduit des changements de phase (voir lissage de l'image).

Voir aussi

• Vision artificielle

Références

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Sobel ».

Lien externe

• (en) Bibliographic citations for Irwin Sobel

• Portail de la photographie
• Portail de l’informatique