Hiérarchie De Chomsky

Hiérarchie De Chomsky: Hiérarchie de Chomsky

La hiérarchie de Chomsky est une classification naturelle (non arbitraire) des langages décrits par les grammaires formelles, découverte en 1956 par le linguiste Noam Chomsky. Tout langage pouvant être généré ou accepté par un système formel (logico-mathématique) peut se définir à l’aide d’une de ces grammaires. Tout système formel pouvant être utilisé pour générer ou accepter un langage quelconque est strictement équivalent à l’une des grammaires formelles de Chomsky.

La hiérarchie de Chomsky constitue le résultat le plus important de la branche primordiale de l’informatique théorique qu’est la théorie des automates. Chaque niveau de grammaire est strictement isomorphe à un type particulier d’automate, le niveau zéro correspondant aux machines de Turing, c’est-à-dire à la puissance de calcul des ordinateurs. La thèse de Church-Turing postule qu’il est impossible de créer une grammaire plus puissante.

Ces travaux sont largement utilisés en informatique, en particulier pour la conception d’interpréteurs ou de compilateurs, ou encore pour l’analyse des langages naturels.

Sommaire

1 Définition

2 Cinq classes de grammaires

2.1 Générales (type 0)

2.2 Contextuelles (type 1)

2.3 Hors-contexte (type 2)

2.4 Réguliers (type 3)

2.5 À choix finis (type 4)

3 Exemples

4 Articles connexes

Définition

La grammaire d’un langage est constituée de quatre objets :

T : ensemble des symboles terminaux, appelé également « alphabet » ou « vocabulaire terminal », noté aussi Σ ;

N : ensemble des symboles non terminaux ;

R : ensemble des règles ;

S (S ∈ N) : axiome (symbole de départ).

Dans la suite on note V = N ∪ T et on suppose que N et T sont disjoints. Les règles définissent les lois d’enchâssement des « mots » du langage, sa grammaire. En français par exemple, la structure sujet + verbe + compléments est un élément de grammaire. Les langages naturels ont une grammaire bien plus complexe que celle des langages de programmation ; il n’est pas possible de la formaliser parfaitement.

Cinq classes de grammaires

Selon Chomsky, les langages sont constitués en 5 classes (type 0 à type 4) hiérarchiquement imbriquées. Les langages de type 0 sont les plus généraux et incluent donc les langages de type 1 (dits "contextuels") qui incluent eux-mêmes les langages de type 2 (dits "hors-contexte") qui incluent eux-mêmes les langages de type 3 (dits "réguliers").

La classification des langages dépend des grammaires qui les engendrent. Ainsi, un langage de type i est engendré par une grammaire de type i. La classification des grammaires est faite en fonction de la forme de leurs règles.

Générales (type 0)

Les règles sont de la forme :

$\alpha \rightarrow \beta$
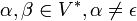
$\alpha, \beta \in V^*, \alpha \neq \epsilon$

Ces grammaires génèrent une classe très grande de mots, mais le temps pour savoir si un mot appartient ou non à celle-ci n'est pas forcément fini. Plus précisément, ces grammaires génèrent les langages dits récursivement énumérables, reconnaissables par machine de Turing : si une phrase appartient à une telle grammaire, on le saura en temps fini; sinon, la machine peut boucler sans donner de réponse. On dit que le problème de l'appartenance d'un mot est alors indécidable.

Contextuelles (type 1)

Les règles sont de la forme :

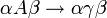
$\alpha A \beta \rightarrow \alpha \gamma \beta$
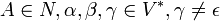
$A \in N, \alpha, \beta, \gamma \in V^*, \gamma \neq \epsilon$

Autrement dit, toute règle comprend un non-terminal entouré de deux mots généraux qui se retrouvent après la dérivation, le non-terminal étant lui-même transformé de façon quelconque (mais non nulle) par la règle de dérivation. Les deux mots à gauche et à droite du non-terminal s'apparentent à un contexte autour de lui. Ces grammaires sont dites contextuelles, car le remplacement d'un élément non-terminal peut dépendre des éléments autour de lui : son contexte. Les langages produits, appelés langages contextuels ou sensibles au contexte, sont exactement ceux reconnus par une machine de Turing linéairement bornée non déterministe. On appelle aussi contextuelles les grammaires dont les règles $\alpha \rightarrow \beta$ sont telles que la longueur de $β$ n'est pas strictement inférieure à celle de $α$ . Car il aisé de voir que ces grammaires produisent exactement les langages contextuels.

Hors-contexte (type 2)

Article détaillé : Grammaire non contextuelle.

Les règles sont de la forme :

$A \rightarrow \gamma$
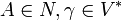
$A \in N, \gamma \in V^*$

Ce sont en réalité des grammaires contextuelles à contexte vide, ce qui signifie que les éléments non-terminaux sont traités individuellement. Ces grammaires produisent exactement les langages hors-contexte, reconnaissables par automate à pile. En France on parle aussi de langages algébriques.

Réguliers (type 3)

Il faut distinguer deux cas (qui sont équivalents).

Les grammaires linéaires gauches. Les règles sont de la forme :

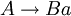
$A \rightarrow Ba$
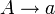
$A \rightarrow a$
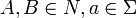
$A,B \in N, a \in \Sigma$

Les grammaires linéaires droites. Les règles sont de la forme :

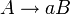
$A \rightarrow aB$
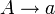
$A \rightarrow a$
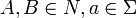
$A,B \in N, a \in \Sigma$

L'ensemble formé par les grammaires linéaires gauche et droite est l'ensemble des grammaires régulières.

Les langages rationnels sont exactement ceux reconnus par automate fini (théorème de Kleene).

Les grammaires linéaires sont des grammaires hors-contextes dont la partie droite de chaque règle contient au plus un symbole non-terminal ; elles constituent une classe intermédiaire entre le type 2 et le type 3. Les règles d'une grammaire linéaire sont de la forme :

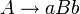
$A \rightarrow aBb$
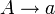
$A \rightarrow a$
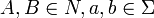
$A,B \in N, a,b \in \Sigma$

À choix finis (type 4)

Les règles sont de la forme :

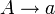
$A \rightarrow a$
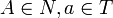
$A \in N, a \in T$
Cette classe, très restreinte, est souvent omise dans la hiérarchie.

Exemples

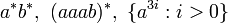Les langages suivants sont réguliers : $a^*b^*,\ (aaab)^*,\ \{a^{3i} : i>0\}$ .

Quelques exemples typiques de langages hors-contexte qui ne sont pas rationnels :

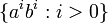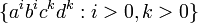$\{a^i b^i : i>0\}\,$ , l'ensemble des palindromes (qui est même un langage linéaire, comme le précédent), l'ensemble des expressions bien parenthésées, comme ( [ ] ( ) ) mais pas ( [ ) ], les expressions arithmétiques parenthésées, $\{a^i b^i c^k d^k : i>0, k>0\}\,$ .

Des exemples de langages contextuels qui ne sont pas hors-contexte :

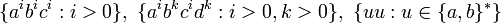$\{a^i b^i c^i : i>0\},\ \{a^i b^k c^i d^k : i>0, k>0\},\ \{uu : u\in\{a,b\}^*\}$ .

Voir aussi les exemples sur la page grammaire formelle. La théorie des langages formels dispose de nombreux outils pour affirmer, ou infirmer, le type d'un langage (rationnel, algébrique etc.). La construction explicite d'une grammaire reconnaissant un langage donné n'est pas toujours facile, quoique de nombreux algorithmes aient été proposés dans la littérature scientifique. On trouvera des références sur ce sujet dans tout bon livre de théorie des langages formels.

Articles connexes

Grammaire formelle

Théorie des automates

Noam Chomsky

Marcel-Paul Schützenberger

Portail de l’informatique

Ce document provient de « Hi%C3%A9rarchie de Chomsky ».

Catégories : Langage formel | Syntaxe | Linguistique générative

Contenu soumis à la licence CC-BY-SA. Source : Article Hiérarchie De Chomsky de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Hierarchie de Chomsky — Hiérarchie de Chomsky La hiérarchie de Chomsky est une classification naturelle (non arbitraire) des langages décrits par les grammaires formelles, découverte en 1956 par le linguiste Noam Chomsky. Tout langage pouvant être généré ou accepté par… … Wikipédia en Français
Hiérarchie de chomsky — La hiérarchie de Chomsky est une classification naturelle (non arbitraire) des langages décrits par les grammaires formelles, découverte en 1956 par le linguiste Noam Chomsky. Tout langage pouvant être généré ou accepté par un système formel… … Wikipédia en Français
Hiérarchie de Chomsky — En informatique théorique, en théorie des langages, et en calculabilité, la hiérarchie de Chomsky est une classification des langages formels et des grammaires formelles, décrite par Noam Chomsky en 1956[1]. Cette section ne cite pas suffisamment … Wikipédia en Français
Chomsky-Hierarchie — Chomsky Hierarchie, gelegentlich Chomsky–Schützenberger Hierarchie (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger), ist ein Begriff aus der Theoretischen Informatik. Sie ist eine Hierarchie von Klassen… … Deutsch Wikipedia
Chomsky Hierarchie — Chomsky Hierarchie, gelegentlich Chomsky–Schützenberger Hierarchie, (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger) ist ein Begriff aus der Theoretischen Informatik und bezeichnet eine Hierarchie von Klassen… … Deutsch Wikipedia
Chomsky-Typ — Chomsky Hierarchie, gelegentlich Chomsky–Schützenberger Hierarchie, (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger) ist ein Begriff aus der Theoretischen Informatik und bezeichnet eine Hierarchie von Klassen… … Deutsch Wikipedia
Chomsky — Noam Chomsky Pour les articles homonymes, voir Chomsky (homonymie). Noam Chomsky Linguiste occidental XXe siècle … Wikipédia en Français
Hiérarchie arithmétique — En logique mathématique, plus particulièrement en théorie de la calculabilité, la hiérarchie arithmétique, définie par Kleene est une hiérarchie des sous ensembles de l ensemble N des entiers naturels définissables dans le langage du premier… … Wikipédia en Français
Chomsky — ist der Name folgender Personen: Aviva Chomsky (* 1957), US amerikanische Historikerin, Tochter von Carol und Noam Chomsky Carol Chomsky (1930–2008), US amerikanische Linguistin Marvin J. Chomsky (* 1929), US amerikanischer Filmregisseur und… … Deutsch Wikipedia
hierarchie — Organisation dans laquelle les elements sont repartis dans une relation de specialisation de sorte que chacun soit superieure (plus general) au suivant (plus particulier). de Chomsky N. Chomsky 1957 distingue quatre classes de grammaires… … Glossaire de linguistique computationnelle

Dictionnaires et Encyclopédies sur 'Academic'

Hiérarchie De Chomsky

Hiérarchie de Chomsky

Sommaire

Définition

Cinq classes de grammaires

Générales (type 0)

Contextuelles (type 1)

Hors-contexte (type 2)

Réguliers (type 3)

À choix finis (type 4)

Exemples

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Hiérarchie De Chomsky

Hiérarchie de Chomsky

Sommaire

Définition

Cinq classes de grammaires

Générales (type 0)

Contextuelles (type 1)

Hors-contexte (type 2)

Réguliers (type 3)

À choix finis (type 4)

Exemples

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link