- Géodésie physique (potentiel de double couche)
-
Potentiel de double couche
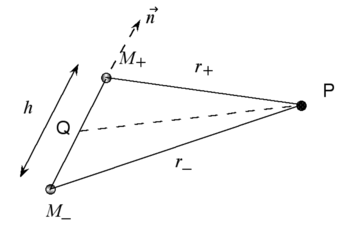
Imaginons en un point potentiant quelconque Q un dipôle gravifique formé de deux masses ponctuelles de signes opposés, M + = + MQ et M − = − MQ, situées de part et d'autre de Q à une distance h / 2.
A priori, le concept d'un tel dipôle gravifique paraît dénué de signification physique, puisque la gravitation s'exerce toujours comme une force d'attraction, non comme une force de répulsion. Cela implique qu'en théorie de la gravitation il n'existe pas de masses négatives, contrairement à ce qui se passe dans les théories de l'électrostatique et de la magnétostatique, où la considération de dipôles électriques et magnétiques est d'une importance capitale. Néanmoins, la notion de dipôle gravifique possède une grande utilité en géodésie physique où l'on est amené à considérer des excès ou des défauts de densité par rapport à une valeur standard, et à raisonner comme si ces excès ou défauts de masse constitueraient en fait des masses additionnelles causant en un point potentié P un « élément de potentiel de double couche » δV2L qui se superpose au potentiel gravifique en P engendré par la distribution de masse standard.
Le potentiel combiné engendré en P par les deux masses du dipôle est, En désignant par r+ la distance de P à M+ et par r– la distance de P à M–, le potentiel combiné engendré en P par les deux masses du dipôle est
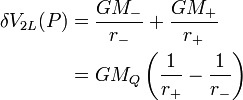
La fonction entre parenthèses est manifestement une fonction de la distance h entre les masses M − et M + , et s'annule avec h. En désignant M − le point occupé par la masse M − , M + celui occupé par la masse M + , nous avons
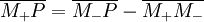
ou encore
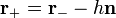 ,
,la direction
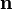 étant le vecteur unitaire pointant de M − à M + .
étant le vecteur unitaire pointant de M − à M + .Lorsque h tend vers 0 on a donc
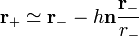 et
et 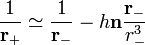 ,
,c'est-à-dire
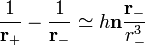 .
.La quantité vectorielle
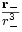 est le gradient de
est le gradient de 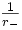 évalué au point M1. L'expression
évalué au point M1. L'expression 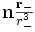 représente donc la dérivée de
représente donc la dérivée de 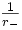 dans la direction
dans la direction 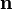 . Nous noterons dans la suite la dérivation dans la direction
. Nous noterons dans la suite la dérivation dans la direction 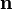 par
par 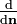 , et nous obtenons par conséquent
, et nous obtenons par conséquent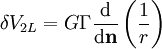
en posant r = r − et Γ(Q) = MQh.
Γ(Q) est le moment dipolaire gravifique au point Q. On suppose que les masses M − et M + grandissent indéfiniment lorsque h tend vers zéro, de manière à donner à ce moment dipolaire une valeur finie. La relation
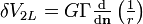 fournit le potentiel d'un tel dipôle élémentaire.
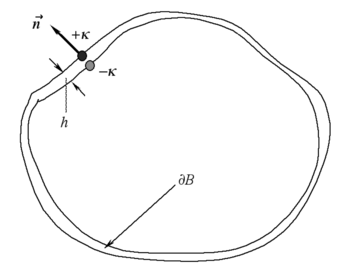
fournit le potentiel d'un tel dipôle élémentaire.On peut se représenter une double couche sur une surface
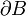 comme deux simples couches séparées par une petite distance h. D'un point de vue mathématique, on considérera cette distance comme infinitésimale. La normale unitaire extérieure à la surface
comme deux simples couches séparées par une petite distance h. D'un point de vue mathématique, on considérera cette distance comme infinitésimale. La normale unitaire extérieure à la surface 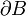 , à savoir
, à savoir 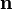 , intersecte les deux couches en deux points M − et M + très proches l'un de l'autre et possédant des densités surfaciques κ de même magnitude, mais de signes opposés. Ainsi, chaque couple de points correspondants (M − ,M + ) forme un dipôle ayant une densité de moment dipolaire gravifique
, intersecte les deux couches en deux points M − et M + très proches l'un de l'autre et possédant des densités surfaciques κ de même magnitude, mais de signes opposés. Ainsi, chaque couple de points correspondants (M − ,M + ) forme un dipôle ayant une densité de moment dipolaire gravifique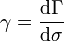
En additionnant les contributions δV2L(P) de tous les dipôles que l'on suppose distribués continument sur la surface
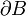 , on obtient le potentiel de double couche :
, on obtient le potentiel de double couche :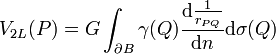 .
.Ce potentiel est continu partout sauf sur la surface
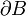 . Sur cette surface, nous obtenons deux limites différentes pour le potentiel, selon que nous nous approchons de l'extérieur ou de l'intérieur de la surface. Du côté extérieur, le potentiel vaut
. Sur cette surface, nous obtenons deux limites différentes pour le potentiel, selon que nous nous approchons de l'extérieur ou de l'intérieur de la surface. Du côté extérieur, le potentiel vaut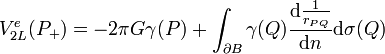
et du côté intérieur, il vaut
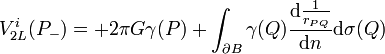
de sorte qu'il présente une discontinuité de
![\Bigl[\Delta V_{2L}(P) \Bigr]_{-}^{+} = V_{2L}^{e}(P_{+}) - V_{2L}^{i}(P_{-}) = -4 \pi G\gamma(P)](/pictures/frwiki/50/221c156ced6cc91ee76d00b7f3e1a182.png)
lorsqu'on passe au point P de l'intérieur à l'extérieur de la surface
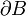 .
.Les relations précédentes pour le potentiel de double couche sont semblables aux relations fournissant la dérivée normale du potentiel de simple couche. Mais il convient de bien comprendre que ces deux types de potentiels associés à une surface matérielle ont, en fait, des comportements très dissemblables, en quelque sorte complémentaires. En effet, le potentiel de simple couche est continu partout, et sa dérivée normale est discontinue sur la surface matérielle. Par contre, le potentiel de double couche est lui-même discontinu sur la surface matérielle, mais sa dérivée normale est continue. Toutefois, à grande distance de la surface matérielle, les deux potentiels ont des comportements analogues, puisqu'ils décroissent comme 1 / r et s'annulent à l'infini.
C'est l'existence d'une discontinuité, dans le potentiel de double couche lui-même d'une part, dans la dérivée normale du potentiel de simple couche d'autre part, qui rend les concepts au départ purement mathématiques de potentiels de simple couche et de double couche si intéressants pour la géodésie, notamment en relation avec les théorèmes de Green.
Bibliographie
Heiskanen, W.A. et H. Moritz, Physical Geodesy, W.H. Freeman and Company, San Francisco and London, 1967, ix + 364 pp.
Voir aussi
Notes
- Portail de la géodésie et de la géophysique
- Portail de la physique
Catégories : Géodésie | Physique mathématique | Milieux continus
Wikimedia Foundation. 2010.