- Groupe des symplectomorphismes
-
Groupe des symplectomorphismes
Le groupe des symplectomorphismes d'une variété symplectique (M,ω), noté Symp(M,ω), dénote l'ensemble des Symplectomorphismes ou difféomorphismes symplectiques de (M,ω), muni de la loi de composition.
Sommaire
Intéret
Propriétes algébriques
Le groupe des symplectomorphismes n'est pas un sous-groupe normal de Diff(M,ω).
Si f est un difféomorphisme de la variété M, la conjugaison par f fait correspondre bijectivement les symplectomorphismes de (M,ω) et de (M,f * ω) :
- f.Symp(M,ω).f − 1 = Symp(M,f * ω)
En particulier, la conjugaison par un difféomorphisme f préserve le sous-groupe Symp(M,ω) si et seulement si f est un symplectomorphisme.
Topologie
Il est pratique de munir le groupe des symplectomorphismes de la topologie
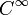. Dans ce cas, Symp(M,ω) apparait comme un sous-groupe fermé du groupe des difféomorphismes Diff(M,ω). Accessoirement, le groupe des difféomorphismes peut en toute légitimité être vu comme un groupe de Lie de dimension infinie. Plus précisément, l'espace tangent en l'identité associée est l'espace de Fréchet X(M) des champs de vecteurs de classe 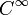sur M.Le groupe des symplectomorphismes est un sous-groupe fermé pour la topologie C0 du groupe des homéomorphismes de la variété M.
La preuve repose sur l'utilisation des capacités symplectiques. Une capacité symplectique est la donnée pour toute variété symplectique (M,ω) d'un réel positif C(M,ω), vérifiant les propriétés suivantes :
En particulier, pour une variété symplectique (M,ω) donnée, le réel C(U) est associé a chaque ouvert U.Articles connexes
Liens externes
Catégorie : Géométrie symplectique
Wikimedia Foundation. 2010.
