Graphe Conceptuel

Un graphe conceptuel est un outil symbolique utilisé dans la théorie des graphes conceptuels. Développée par Sowa (1984), cette théorie est un formalisme général de représentation de connaissances fondé sur la logique ; elle s'inscrit dans la continuité des graphes existentiels de Charles Sanders Peirce. C'est aussi un langage de représentation de connaissances basé sur la linguistique, la psychologie et la philosophie. Il a été conçu dans l'objectif de développer un système de logique qui représente de façon plus simple et plus commode les structures du langage naturel.

Sommaire 1 Introduction au modèle 2 Graphe conceptuel et réseau sémantique 3 Structuration conceptuelle 4 Notion de canon : Raisonnement dans un monde ouvert 5 Représentation contextuelle 6 Transformation en logique 7 Apports et limites 8 Bibliographie 9 Voir aussi

Introduction au modèle

Le modèle est construit sur les bases de la perception qui génère, dans un modèle de travail, une construction qui représente une entrée sensorielle. La perception est basée sur les mécanismes suivants :

• Une stimulation est enregistrée dans une forme appelée un icône sensoriel,
• Un comparateur associatif recherche en mémoire les percepts représentant tout ou partie de l'icône
• Un assembleur réunit les percepts dans un modèle de travail qui forme une approximation finie de l'entrée. Un enregistrement de l'assemblage est stocké sous forme de graphe conceptuel
• Des mécanismes conceptuels recherchent des concepts concrets qui sont associés aux percepts et des concepts abstraits qui n'ont pas de percepts associés

D'après Sowa (1984), les graphes conceptuels sont des graphes finis, connectés et bipartis.

• Les deux sortes de nœuds d'un graphe biparti sont les concepts et les relations conceptuelles,
• Chaque relation conceptuelle possède un arc ou plus, chacun d'entre eux doit être lié à un concept,
• Si une relation a n arcs, elle est dite n-adique,
• Un unique concept peut former un graphe conceptuel, mais chaque arc de chaque relation conceptuelle doit être lié à un concept quelconque.

Il existe deux types de notations. La notation graphique, de lisibilité simple, et la notation linéaire proche de l'implantation en logique du premier ordre.

Graphe conceptuel et réseau sémantique

Un graphe conceptuel n'a pas de sens isolément. C'est seulement au travers d'un réseau sémantique que les concepts et les relations sont reliés au contexte, langage, émotion, et perception :

• les concepts concrets sont associés aux percepts pour éprouver la situation réelle et aux mécanismes moteurs pour agir dessus,
• certains concepts sont associés à des mots et des règles de grammaire du langage,
• une hiérarchie de types de concept définit les relations entre concepts à différents niveaux de généralité,
• des règles de constitution déterminent comment chaque type de concept doit être lié aux relations conceptuelles,
• chaque graphe conceptuel est lié à un contexte ou épisode duquel il dépend,
• Chaque épisode doit aussi avoir des associations émotionnelles, qui indirectement confèrent des nuances émotionnelles aux types de concepts impliqués.

Structuration conceptuelle

La hiérarchie de type de concepts, supporte les propriétés d'héritage des super-types vers les sous-types de concepts dont l’origine remonte à Aristote (théorie des catégories et syllogismes), une méthode pour définir les nouveaux types par genre (genus) et par différence spécifique (differentiae), et l'utilisation de syllogismes pour analyser les propriétés d'héritage. Sowa introduit, dans sa théorie, les notions de super-type commun minimal et sous-type commun maximal permettant de passer d’une hiérarchie conceptuelle à un treillis conceptuel. La théorie des graphes conceptuels supporte la classification aristotélicienne ainsi que la classification par ressemblance de famille représentée respectivement par des schémas et des prototypes.

Notion de canon : Raisonnement dans un monde ouvert

Eu égard aux contraintes sélectives sur les possibilités de combinaisons de mots, Sowa a introduit la notion de graphe canonique pour contraindre son modèle à la théorie des sémantiques développée par Katz et Fodor.

De plus, le canon (base de graphes canoniques) peut s’enrichir des connaissances acquises au fur et à mesure de l’expérience du système. Pour ce faire, quatre opérations sont nécessaires : la copie d’un graphe, la restriction conceptuelle, la jointure de graphes et la simplification de graphes. Ces opérations sont à l’inverse des règles d’inférences ; c’est un principe de règles de réfutation permettant d’étendre le modèle dans un monde ouvert en ayant une base de connaissances de faits vrais et une base de connaissances de faits faux.

Représentation contextuelle

Les graphes conceptuels n'imposent aucune contrainte alors que les graphes canoniques introduisent des contraintes sélectives qui correspondent au cas des frame en linguistique et des contraintes catégorielles en philosophie.

Les schémas introduisent les connaissances spécifiques d'un domaine ; ils représentent les connaissances plausibles.

Transformation en logique

Un opérateur transforme des graphes conceptuels (notation linéaire) en formules de calcul prédicatives du premier ordre. Lors de la transformation d'un graphe en formule prédicative, les concepts individuels sont transformés en constantes, les concepts génériques sont transformés en variables.

Cette approche permet tout autant le raisonnement inverse : à partir d'une formulation logique, nous pouvons construire un graphe conceptuel. Cette inversion est pertinente dans le cadre des études formelles telles que les politiques de sécurité. L'exemple suivant représente, en graphe conceptuel l'axiome K de l'Obligation définit suivant SDL (Standard Deontic Logic) utilisant une logique modale KD pour l'obligation :

Représentation en logique :

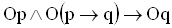
Représentation en graphe :

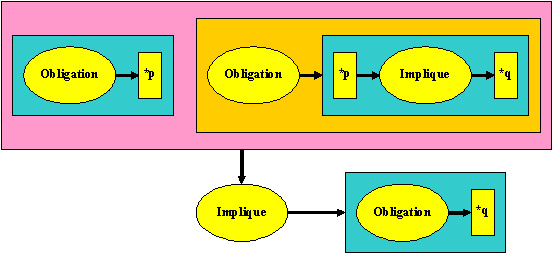
Avec p et q qui sont des propositions.

Apports et limites

Les graphes conceptuels, par leur représentation graphique, sont d’un abord simple. La notation linéaire issue de la représentation graphique impose certaines connaissances propres à une syntaxe plus riche donc plus difficile à acquérir.

Ce système de représentation est souple, ce qui permet de se rapprocher de l’efficacité descriptive du langage naturel et possède un bon niveau de rigueur. Il prend en compte de multiples contraintes linguisitiques et philosophiques : la notion de dénotation, de substituts nominaux, d’appartenance à un ensemble, d’abstraction, etc. Les graphes conceptuels, par des opérations de spécialisation et de généralisation, possèdent entre eux une hiérarchie de graphes sur laquelle s'applique une relation d'ordre partielle.

Les graphes conceptuels sont plus expressifs que la logique du premier ordre par l’introduction de modalités (relations conceptuelles monadiques) et la prise en compte des ensembles.

Le problème majeur des graphes est leur décidabilité : savoir s’il existe une projection (opération de spécialisation) entre deux graphes est intrinsèquement exponentielle. Quelques cas particuliers tels que les graphes acycliques sont décidables. Ce problème met en évidence les temps prohibitifs de calcul que nous rencontrons dans les réseaux sémantiques.

Bibliographie

• Chomsky N. - Syntactic structures, Mouton, La Haye (Traduction française : structures syntaxiques, 1959, Le Seuil, Paris)., 1957
• Katz J. J., Fodor J. A. - The structure of a semantic theory, Language, 39, 1963
• Sowa, J.F. - Conceptual Graphs for a Data Base Interface, IBM Journal of Research and Development 20(4), 336–357, 1976.(Fichier PDF)
• Sowa J. F. - Conceptual Structures : Information Processing in Mind and Machine, Addison-Wesley, (ISBN 0-20114-472-7), 1984
• Chein M., Mugnier M.-L. – Conceptual Graphs : Fundamental Notions, Revue d’Intelligence Artificielle Volume 6 n^o 4, 1992
• Kayser D. – La Représentation des Connaissances, Hermes, (ISBN 2-86601-647-5), 1997

Voir aussi

• Schéma conceptuel