Grandissement (optique)

Grandissement (optique)

Grandissement

En optique la notion de grandissement (noté γ) est associée au rapport d'une grandeur de l'objet à son équivalent pour l'image de cet objet à travers un système optique. Elle se note X.X : le premier chiffre est la taille relative au sujet de l'image qui se forme sur la surface sensible et le second est la taille du sujet. C'est une grandeur sans dimension, qui permet de relier :

  • les tailles de l'objet et de l'image : grandissement transversal,
  • les angles sous lesquels sont un objet et son image : grandissement angulaire,
  • les positions respectives de l'objet et de l'image sur l'axe optique : grandissement longitudinal.

Soit AB l'objet et A'B' l'image de cet objet donnée par une lentille mince convergente.

On a alors la relation suivante :

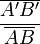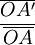
γ = \overline{A'B'}\over\overline{AB} = \overline{OA'}\over\overline{OA}

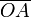\overline{OA}  : la distance entre le point A et le centre optique O de la lentille ;

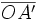\overline{OA'} : la distance entre le point A' (image de A par la lentille) et le centre optique de la lentille ;

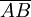\overline{AB} : la hauteur de l'objet AB ;

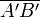\overline{A'B'} : la hauteur de l'image A'B' ;

Remarque : Le grandissement s'exprime sans unité.

Propriétés

Si γ > 0 alors l'image est droite (elle a le même sens que l'objet)

Si γ < 0 alors l'image est renversée (sens inverse)

Si |γ| > 1 alors l'image est plus grande que l'objet

Si |γ| < 1 alors l'image est plus petite que l'objet

Si l'on considère une lentille mince convergente de distance focale f' et un objet AB placé à d = 2*f' du centre optique de cette lentille alors l'image A'B' apparaîtra après la lentille à la même distance d et on aura pour le grandissement : γ = - 1. Une application de cette propriété est la Méthode de Silbermann en focométrie.

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Grandissement ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Grandissement (optique) de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • grandissement — [ grɑ̃dismɑ̃ ] n. m. • 1845; de grandir ♦ Vieilli Fait de devenir plus grand, action de rendre plus grand. ⇒ agrandissement. ♢ Opt. Rapport des dimensions d un objet à son image donnée par un système optique. ⇒ grossissement. ● grandissement nom… …   Encyclopédie Universelle

  • Optique metaxiale — Optique métaxiale L optique métaxiale constitue une synthèse entre l optique géométrique et l optique physique. Elle a pour spécificité de rendre compte simultanément du phénomène d’imagerie du couple Champ Cohérence, ainsi que de ses… …   Wikipédia en Français

  • OPTIQUE - Optique instrumentale — On appelle «instrument d’optique» tout système formant l’image d’un objet sur un ou plusieurs récepteurs sensibles à la lumière et dont le rôle est de percevoir ou d’exploiter cette image. Par exemple, une lunette comporte plusieurs lentilles… …   Encyclopédie Universelle

  • OPTIQUE - Images optiques — Les «pièces optiques» (lentilles et parfois miroirs), seules ou convenablement associées – on dira dans tous les cas les «systèmes optiques» –, permettent d’obtenir d’un objet, lumineux par lui même ou parce qu’il est convenablement éclairé, une… …   Encyclopédie Universelle

  • Optique geometrique — Optique géométrique L optique géométrique est une branche de l optique qui s appuie notamment sur la notion de rayon lumineux. Cette approche simple permet notamment des constructions géométriques d images qui lui confèrent son nom. Sommaire 1… …   Wikipédia en Français

  • OPTIQUE - Principes physiques — Toute classification des domaines de l’optique est en partie arbitraire et comporte de nombreux recouvrements. L’optique géométrique s’appuie essentiellement sur la notion de rayons lumineux susceptibles de fournir des images qu’on observe à… …   Encyclopédie Universelle

  • OPTIQUE - Optique électronique — L’optique électronique ou plus généralement l’optique corpusculaire s’intéresse aux trajectoires d’électrons libres accélérés, et à tous les procédés permettant de guider ces particules dans un espace où règne un vide poussé. On peut en effet se… …   Encyclopédie Universelle

  • Grandissement — En optique la notion de grandissement (noté γ) est associée au rapport d une grandeur de l objet à son équivalent pour l image de cet objet à travers un système optique. Elle se note X.X : le premier chiffre est la taille relative au sujet… …   Wikipédia en Français

  • Optique métaxiale — L optique métaxiale constitue une synthèse entre l optique géométrique et l optique physique. Elle a pour spécificité de rendre compte simultanément du phénomène d’imagerie du couple Champ Cohérence, ainsi que de ses transformations… …   Wikipédia en Français

  • Optique géométrique — L optique géométrique est une branche de l optique qui s appuie notamment sur la notion de rayon lumineux. Cette approche simple permet notamment des constructions géométriques d images qui lui confèrent son nom. Sommaire 1 Introduction 1.1 Place …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”