Gordon Shapiro

Gordon Shapiro

Méthode de Gordon et Shapiro

La méthode de Gordon et Shapiro est un modèle d'actualisation des actions. Il porte le nom de ses auteurs et a été mis au point en 1956.

Ce modèle, dit aussi de « croissance perpétuelle », ne tient pas compte des plus values. En effet, il considère que lorsque le flux de dividendes est perpétuel (c’est-à-dire qu'il tend vers l'infini), la plus value n'a pas d'incidence sur l'évaluation de l'action.

Sommaire

Description

Le modèle

La formule proposée par Gordon et Shapiro est la suivante : 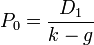P_0=\frac{D_1}{k-g} dans laquelle :

  • P0 = valeur théorique de l'action
  • D1 = dividende anticipé de la première période
  • k = Taux de rendement attendu pour l'actionnaire
  • g = Taux de croissance des dividendes

Démonstration

On part du modèle de Durand qui étend les formules d'évaluation des actifs à l'univers incertain: le prix d'une action aujourd'hui (P0) est égale à la somme de ses cash-flows actualisés au taux de la période (kt) c'est-à-dire ses dividendes (Dt) versés à chaque période t ainsi que son prix de revente futur (PT):

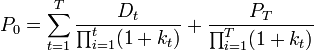
P_0 = \sum_{t=1}^T \frac{D_t}{ \prod_{i=1}^t (1+ k_t)} + \frac{P_T}{ \prod_{i=1}^T (1+ k_t)}

Or le prix de revente en T sera égal à cette même formule et ce ainsi de suite jusqu'à l'infini, car une action n'a pas vocation à être remboursée. En finance, on suppose souvent que le taux d'actualisation est le même à chaque période c'est-à-dire que k1 = kt = k (sinon, on utilisera une moyenne géométrique des taux sur la totalité des périodes). On en déduit alors:

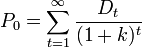
P_0 = \sum_{t=1}^\infty \frac{D_t}{(1+ k)^t}

Gordon et Shapiro supposent qu'à chaque période, le dividende versé est une fraction constante des bénéfices de l'entreprise: Dt = αBt. On suppose également que les bénéfices croissent chaque période au même taux, donc les dividendes croissent aussi selon un même taux noté g, d'où:

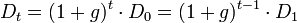
D_t = (1+g)^t \cdot D_0 = (1+g)^{t-1} \cdot D_1

En appliquant ce que l'on vient de montrer dans le modèle de Durand:

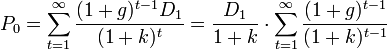
P_0 = \sum_{t=1}^\infty \frac{(1+g)^{t-1} D_1}{(1+k)^t} = \frac{D_1}{1+k} \cdot \sum_{t=1}^\infty \frac{(1+g)^{t-1} }{(1+k)^{t-1} }

On sait que pour toute suite de raison q, sa série (somme des termes de cette suite) à l'infini est égale à: 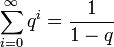\sum_{i=0}^\infty q^i = \frac{1}{1-q}, donc ici: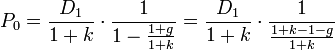

P_0 = \frac{D_1}{1+k} \cdot \frac{1}{1 - \frac{1+g}{1+k}} = \frac{D_1}{1+k} \cdot \frac{1}{\frac{1+k-1-g}{1+k}}

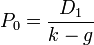
P_0 = \frac{D_1}{k-g}

Extensions

Calcul du taux de croissance des dividendes

Pour déterminer le taux de croissance des dividendes, nous utiliserons deux observations :

  • les données historiques de l'action ;
  • les prévisions des analystes sur les futurs dividendes.

On remarquera que Kc doit être supérieur à g pour que le modèle fonctionne. Autrement dit, le taux de rendement attendu par les actionnaires doit être supérieur aux taux de croissance des dividendes.

Exemple :
Soit une société Alpha, dont les investisseurs estiment que ses résultats ainsi que son dividende devraient doubler en l'espace de 5 ans. La rentabilité exigée par les actionnaires est de 20% et le dernier dividende versé est de 5 euros par action.

g, le taux de croissance du dividende est alors calculé de la manière suivante :
soit D0, le dividende actuel et D5, le dividende dans 5 ans. Le dividende devant doubler en 5 ans, on a : D5= 2 D0, c'est-à-dire (1+g)5D0 = 2 D0 et par conséquent, g ≈ 0,1487.

Le taux de croissance des dividendes est donc égal à 14,87% pour les 5 prochaines années. L'hypothèse que ce taux de croissance est perpétuel permet d'appliquer la formule de Gordon et Shapiro.

La valorisation théorique de l'action suivant la formule de Gordon et Shapiro sera donc de : 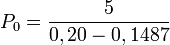P_0=\frac{5}{0,20-0,1487} euros, soit 97,46 euros.

Comparaisons

Utilisation pour comparer des actions entre elles

Une façon plus intéressante d'utiliser le modèle est de mener des comparaisons entre actions. La méthode sera d'autant plus valable que la comparaison sera effectuée entre des entreprises comparables en termes de secteurs. Prenons un exemple pour bien comprendre :

Exemple : Soit trois sociétés, A, B et C. Pour chacune d'elles nous avons collecté les données suivantes. Nous avons aussi calculé "g", le taux de croissance des dividendes, au préalable.

Cours de l'action P0) Dividende(D) BNPA g :

  • Société A 25 2 3 5%
  • Société B 70 6 8 6%
  • Société C 300 15 25 5,5%


Afin d'avoir une première idée de la valorisation de ses trois sociétés les unes par rapport aux autres, nous pouvons appliquer la méthode des PER. Pour mémoire, le PER est le rapport entre le cours de l'action et le bénéfice net par action BNPA.


PER

  • Société A 8,3
  • Société B 8,7
  • Société C 12


Plus le PER est élevé, plus la valeur est considérée comme chère. Dans cet exemple, c'est la société A qui apparaît comme la moins bien valorisée, alors que C est la plus chère.

Passons à présent au modèle de Gordon et Shapiro, son côté dynamique et axé sur les dividendes futurs, nous permettra peut être de mettre en lumière d'autres éléments.

La formule initiale nous propose : P0 = D / (Kc - g)

En la remaniant on obtient la forme suivante : Kc = g + (D / P0) appliquons là à nos trois sociétés avec les données du tableau.

Kc Kc

  • Société A 5% + (2 / 25) 13%
  • Société B 6% + (6 / 70) 14,6%
  • Société C 5,5% + (15 / 300) 10,5%


A la lumière du taux de rentabilité, il apparaît que c'est la société B qui possède le profil le plus intéressant. Étant très proche en termes de PER de la société A, nous aurons tendance à préférer cet investissement dans une optique de moyen-long terme.

Conclusion : dans le modèle de Gordon et Shapiro, on part du postulat que les dividendes vont croître indéfiniment à un taux de croissance constant. Ceci introduit par conséquent des limites au modèle. En effet, il est très rare que ce taux puisse être constant, tout du moins à l'infini.

Par ailleurs, la formule ne reste valable qu'à nombre d'actions constant. Dans le cas contraire (très fréquent) il faudra réajuster nos données.

Limites du modèle

Le modèle de Gordon-Shapiro applique l'analyse des titres financiers à revenus certains dans un univers incertain.

Un premier reproche concerne l'évolution dans le temps des bénéfices: Gordon-Shapiro n'est absolument pas capable de prendre en compte les variations des bénéfices donc des dividendes (volatilité).

Que peut-on dire également d'une entreprise qui ne distribue aucun dividende ? Le prix de l'action serait ici nul, or il est évident que ceci n'est pas vérifié empiriquement.

Lorsque le taux de rendement s'égalise au taux de croissance, le prix de l'action tend vers l'infini, est-ce viable ?

Le modèle a cependant pour lui l'avantage de la simplicité, il est donc largement répandu dans les milieux financiers. Néanmoins, il repose sur des hypothèses figées et restrictives et devra être pondéré dans l'exploitation de ses résultats. Il nous permettra de mettre en lumière des différences dans la valorisation des actions, il ne sera jamais utilisé seul mais en complément d'une autre analyse.


  • Portail de la finance Portail de la finance
  • Portail de l’économie Portail de l’économie
Ce document provient de « M%C3%A9thode de Gordon et Shapiro ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Gordon Shapiro de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Modelo Gordon-Shapiro — El modelo de Gordon Shapiro, también conocido como el modelo de dividendos crecientes a tasas constantes, es una variación del modelo de análisis de flujos de caja descontados, usado para avaluar acciones o empresas. Este modelo presupone un… …   Wikipedia Español

  • SHAPIRO, ALEXANDER M. — SHAPIRO, ALEXANDER M. (1929–1992), U.S. Conservative rabbi. Shapiro was born in Brooklyn, N.Y., and received a B.A. from Brooklyn College as well as a B.H.L. from the jewish theological seminary , in 1950. He was ordained at JTS in 1955 and… …   Encyclopedia of Judaism

  • Gordon Denlinger — Gordon R. Denlinger Member of the Pennsylvania House of Representatives from the 99th district Incumbent Assumed office March 18, 2003 Preceded by Leroy Zimmerman Personal detail …   Wikipedia

  • Gordon Michael Woolvett — (* 12. Juni 1970 in Hamilton, Ontario) ist ein kanadischer Schauspieler. Er ist mit Michele Morand verheiratet und hat zwei Söhne, Rogan (geboren 31. Juli 2001) und Griffin James (geboren Anfang November 2008) sowie eine Tochter, Veronica Michele …   Deutsch Wikipedia

  • Gordon Pettengill — (born 1926) is a noted American radio astronomer and planetary physicist. Early life and education Pettengill was born in Providence, Rhode Island. As a young man he was enthralled with radio and electronics, taking apart and building old radios …   Wikipedia

  • Gordon Michael Woolvett — est un acteur et scénariste canadien né le 12 juin 1970 à Hamilton (Canada). Sommaire 1 Biographie 2 Filmographie 2.1 comme acteur 2.2 …   Wikipédia en Français

  • Gordon Davidson — For the Australian Senator, see Gordon Davidson (Australian politician). Gordon Davidson (7 May 1933, Brooklyn, New York) is an American stage and film director. External links Gordon Davidson at the Internet Broadway Database Gordon Davidson at… …   Wikipedia

  • Methode de Gordon et Shapiro — Méthode de Gordon et Shapiro La méthode de Gordon et Shapiro est un modèle d actualisation des actions. Il porte le nom de ses auteurs et a été mis au point en 1956. Ce modèle, dit aussi de « croissance perpétuelle », ne tient pas… …   Wikipédia en Français

  • Méthode De Gordon Et Shapiro — La méthode de Gordon et Shapiro est un modèle d actualisation des actions. Il porte le nom de ses auteurs et a été mis au point en 1956. Ce modèle, dit aussi de « croissance perpétuelle », ne tient pas compte des plus values. En effet,… …   Wikipédia en Français

  • Méthode de gordon et shapiro — La méthode de Gordon et Shapiro est un modèle d actualisation des actions. Il porte le nom de ses auteurs et a été mis au point en 1956. Ce modèle, dit aussi de « croissance perpétuelle », ne tient pas compte des plus values. En effet,… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”