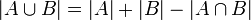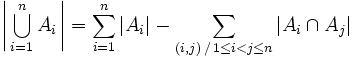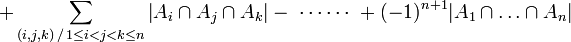Formule du crible

Principe d'inclusion-exclusion

Exemple d'inclusion-exclusion à partir de trois ensembles.

En combinatoire, le principe d’inclusion-exclusion permet d’exprimer le nombre d’éléments (ou cardinal) d'une réunion finie d'ensembles finis en fonction du nombre d'éléments de ces ensembles et de leurs intersections. Il se traduit directement en termes de probabilités.

Il est attribué au mathématicien Abraham de Moivre, et connu également (lui ou sa version probabiliste) sous le nom de formule du crible de Poincaré, formule de Poincaré, ou formule du crible.

Sommaire

1 Le cas deux ensembles
- 1.1 Exemple
- 1.2 Formule pour n = 2
2 Cas général
3 Version probabiliste
4 Applications

Le cas deux ensembles

Exemple

Parmi 20 étudiants, 10 étudient les mathématiques, 11 étudient la physique, et 4 étudient les deux. Combien y a-t-il d’étudiants qui n’étudient ni les mathématiques ni la physique ?

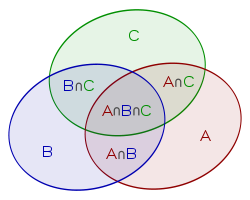
Pour visualiser nous pouvons construire un diagramme de Venn.

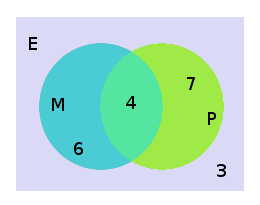
Inclusion exclusion.png

Nous entourons les éléments qui vérifient la même propriété. E représente le groupe entier d’étudiants, M représente ceux qui ont la propriété d'« étudier les mathématiques », P représente ceux qui possède la propriété : d'« étudier la physique ».

Nous plaçons dans chaque partie le nombre d’étudiants. Étant donné que quatre personnes étudient à la fois les mathématiques et la physique, nous reportons un 4 dans l’intersection des deux cercles. Nous devons donc avoir 10-4=6 personnes qui étudient les mathématiques mais pas la physique et 11-4=7 personnes qui étudient la physique mais pas les mathématiques. Il reste donc 20-(6+4+7)=3 personnes qui n’étudient ni les mathématiques ni la physique.

Ce résultat se retrouve facilement en utilisant le principe d’inclusion-exclusion qui donne le nombre d’étudiants ne possédant pas ces deux propriétés 20-10-11+4=3.

Formule pour n = 2

Soient A et B deux ensembles finis, la formule s'écrit

$|A\cup B|=|A|+|B|-|A\cap B|$

où |A| et |B| représentent les cardinaux respectifs de A et B.

En d’autres termes, nous pouvons compter les éléments de la réunion de deux ensembles A et B en additionnant les cardinaux de ces deux ensembles et en soustrayant le cardinal de leur intersection.

Cas général

Soient A₁, ..., A_n n ensembles finis. Nous avons

$\left|\,\bigcup_{i=1}^n A_i\,\right|=\sum_{i=1}^n\left|A_i\right| -\sum_{(i,j)\,/\,1\leq i<j\leq n}\left|A_i\cap A_j\right|$ $+\sum_{(i,j,k)\,/\,1\leq i<j<k\leq n}\left|A_i\cap A_j\cap A_k\right|-\ \cdots\cdots\ +(-1)^{n+1}|A_1\cap\ldots\cap A_n|$

où |A| désigne le cardinal d'un ensemble fini A.

Cette formule peut aussi s'écrire de façon plus condensée

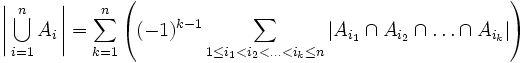$\left|\,\bigcup_{i=1}^n A_i\,\right|=\sum_{k=1}^n \left((-1)^{k-1} \sum_{1\leq i_1<i_2<\ldots<i_k\leq n} \left|A_{i_1}\cap A_{i_2}\cap \ldots \cap A_{i_k}\right|\right)$ .

Elle peut se démontrer par récurrence sur n, ou en utilisant les fonctions indicatrices.

Soit E un ensemble fini, contenant les ensembles A_i. On déduit par passage au complémentaire le cardinal de l'ensemble des éléments de E qui n'appartiennent à aucun des A_i :

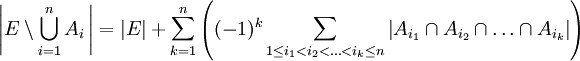$\left|E\setminus\bigcup_{i=1}^n A_i\,\right|=|E|+\sum_{k=1}^n \left((-1)^{k} \sum_{1\leq i_1<i_2<\ldots<i_k\leq n} \left|A_{i_1}\cap A_{i_2}\cap \ldots \cap A_{i_k}\right|\right)$ .

Le principe d’inclusion-exclusion peut se déduire d'une formule d'inversion de Möbius.

Version probabiliste

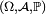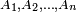Soient un espace probabilisé $\scriptstyle\ (\Omega,\mathcal{A},\mathbb{P})\$ et $\scriptstyle\ n\$ éléments $\scriptstyle\ A_1, A_2, \dots,A_n\$ de la tribu 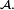$\scriptstyle\ \mathcal{A}.\$ Nous avons

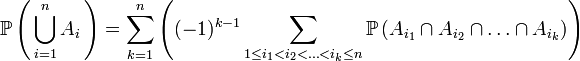$\mathbb{P}\left(\,\bigcup_{i=1}^n A_i\,\right)=\sum_{k=1}^n \left((-1)^{k-1} \sum_{1\leq i_1<i_2<\ldots<i_k\leq n} \mathbb{P}\left(A_{i_1}\cap A_{i_2}\cap \ldots \cap A_{i_k}\right)\right)$ .

Cette formule peut se démontrer par récurrence sur n, ou en utilisant des fonctions indicatrices, de la même manière que la formule précédente.

Applications

Le terme d'ordre k de la somme décroit (en valeur absolue) en fonction de k. Les sommes partielles des premiers termes de la formule fournissent donc alternativement un majorant et un minorant de la somme complète, et peuvent être utilisées comme approximations de celle-ci.

En combinatoire, la formule du crible permet de déterminer le nombre de dérangements d'un ensemble fini. Un dérangement d'un ensemble A est une bijection de A sur lui-même sans point fixe. Grâce au principe d'inclusion-exclusion de Moivre, nous pouvons prouver que si le cardinal de A est égal à n, alors le nombre de dérangements de A est le nombre entier le plus proche de 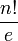$\frac{n!}{e}$ (où e désigne la base des logarithmes népériens).

Il s'ensuit que si toutes les bijections ont la même probabilité d'être choisies, alors la probabilité pour qu'une bijection prise au hasard soit un dérangement tend rapidement vers 1/e lorsque n tend vers l'infini.

Portail des mathématiques

Ce document provient de « Principe d%27inclusion-exclusion ».

Catégorie : Analyse combinatoire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule du crible de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Formule Du Crible De Poincaré — Principe d inclusion exclusion Exemple d inclusion exclusion à partir de trois ensembles. En combinatoire, le principe d’inclusion exclusion permet d’exprimer le nombre d’éléments (ou cardinal) d une réunion finie d ensembles finis en fonction du … Wikipédia en Français
Formule du crible de Poincare — Principe d inclusion exclusion Exemple d inclusion exclusion à partir de trois ensembles. En combinatoire, le principe d’inclusion exclusion permet d’exprimer le nombre d’éléments (ou cardinal) d une réunion finie d ensembles finis en fonction du … Wikipédia en Français
Formule du crible de Poincaré — Principe d inclusion exclusion Exemple d inclusion exclusion à partir de trois ensembles. En combinatoire, le principe d’inclusion exclusion permet d’exprimer le nombre d’éléments (ou cardinal) d une réunion finie d ensembles finis en fonction du … Wikipédia en Français
Formule du crible de poincaré — Principe d inclusion exclusion Exemple d inclusion exclusion à partir de trois ensembles. En combinatoire, le principe d’inclusion exclusion permet d’exprimer le nombre d’éléments (ou cardinal) d une réunion finie d ensembles finis en fonction du … Wikipédia en Français
Crible (Mathématiques) — Pour les articles homonymes, voir Crible. Article détaillé : Théorie des cribles. En mathématiques, les cribles sont des techniques algorithmiques permettant d approcher le cardinal de certains ensembles de nombres. D autre part, ils… … Wikipédia en Français
Crible (mathématiques) — Pour les articles homonymes, voir Crible. Article détaillé : Théorie des cribles. En mathématiques, les cribles sont des techniques algorithmiques permettant d approcher le cardinal de certains ensembles de nombres. D autre part, ils… … Wikipédia en Français
Formule Pour Les Nombres Premiers — Formules pour les nombres premiers En mathématiques, la recherche de formules exactes donnant tous les nombres premiers (ou même donnant uniquement des nombres premiers) s est généralement avérée vaine, ce qui a amené à se contenter de formules… … Wikipédia en Français
Formule pour les nombres premiers — Formules pour les nombres premiers En mathématiques, la recherche de formules exactes donnant tous les nombres premiers (ou même donnant uniquement des nombres premiers) s est généralement avérée vaine, ce qui a amené à se contenter de formules… … Wikipédia en Français
Histoire De La Fonction Zeta De Riemann — Histoire de la fonction zêta de Riemann Cet article présente une histoire de la fonction zêta de Riemann. Pour une présentation mathématique de la fonction et de ses propriétés, voir : Article principal : fonction zêta de Riemann. Un… … Wikipédia en Français
Histoire de la fonction Zeta de Riemann — Histoire de la fonction zêta de Riemann Cet article présente une histoire de la fonction zêta de Riemann. Pour une présentation mathématique de la fonction et de ses propriétés, voir : Article principal : fonction zêta de Riemann. Un… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formule du crible

Principe d'inclusion-exclusion

Sommaire