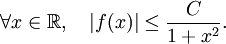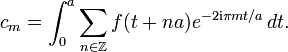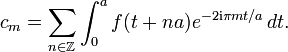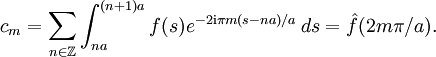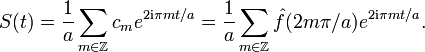Formule de sommation de Poisson

Formule de sommation de Poisson

Formule sommatoire de Poisson

Page d'aide sur l'homonymie Pour les articles homonymes, voir Poisson (homonymie).

La formule sommatoire de Poisson, parfois appelée resommation de Poisson, établit une relation entre le spectre de l'opérateur de Laplace-Beltrami sur le cercle et les longueurs des géodésiques périodiques sur cette courbe. Elle a été découverte par Siméon Denis Poisson.

Sommaire

Formule sommatoire de Poisson

Notations

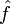Soit une fonction f\, dont la transformée de Fourier est notée \hat{f}, c’est-à-dire :

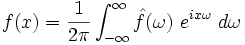f(x) = {1\over 2\pi}\int_{-\infty}^{\infty} \hat{f}(\omega) \ e^{ i x \omega} \ d \omega ,
et 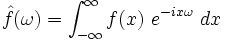\hat{f}(\omega) = \int_{-\infty}^{\infty} f(x) \ e^{- i x \omega} \ dx .

Théorème

Soit f une fonction complexe sur \R deux fois continûment différentiable ; on suppose que f et ses deux premières dérivées sur \R sont intégrables, et qu'elle satisfait l'estimation

\forall x\in \R,\quad |f(x)|\le \frac{C}{1+x^2}.

Soit a un nombre strictement positif. Notons ω0 = 2π / a, le mode fondamental, et 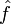\hat f la transformée de Fourier de f. Alors, on a l'identité suivante:

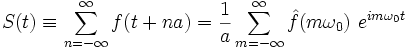S(t) \equiv \sum_{n=-\infty}^{\infty} f(t + n a) = \frac{1}{a} \sum_{m=-\infty}^{\infty} \hat{f}(m \omega_0) \ e^{i m \omega_0 t} .

Démonstration de la formule

Le membre de gauche de la formule sommatoire de Poisson est la somme d'une série de fonctions continues. L'hypothèse faite sur le comportement de f à l'infini implique que cette série converge normalement sur tout \R. Par conséquent, sa somme est une fonction continue, et la formule de définition montre qu'elle est périodique de période a.

Nous pouvons donc calculer les coefficients de sa série de Fourier en exponentielles complexes:

c_m=\int_0^a \sum_{n\in\Z} f(t+na)e^{-2\mathrm{i}\pi mt/a}\, dt.

Du fait de la convergence normale de la série définissant S, on peut échanger intégration et sommation, et écrire ainsi

c_m=\sum_{n\in\Z}\int_0^a f(t+na) e^{-2\mathrm{i}\pi mt/a}\, dt.

Si on effectue dans chaque intégrale le changement de variable t+na=s, on obtient

c_m=\sum_{n\in\Z}\int_{na}^{(n+1)a} f(s) e^{-2\mathrm{i}\pi m(s-na)/a}\, ds=\hat f(2m\pi/a).

D'après nos hypothèses sur f et ses dérivées, et les identités classiques sur la transformée de Fourier d'une dérivée, on voit que la fonction 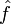\hat f vérifie l'estimation

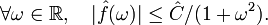\forall \omega\in \R, \quad |\hat f(\omega)|\le \hat C/(1+\omega^2)..

Par conséquent, la série des cm est absolument convergente ; on est dans une situation où on peut sommer la série de Fourier de S, et on obtient

S(t)=\frac{1}{a}\sum_{m\in \Z}c_m e^{2\mathrm{i}\pi mt/a}=\frac{1}{a}\sum_{m\in\Z}\hat f(2m\pi/a) e^{2\mathrm{i}\pi mt/a}.

C'est la formule désirée, modulo le remplacement de 2π / a par ω0.

Convention alternative

Si on utilise les conventions suivantes :

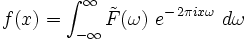f(x) = \int_{-\infty}^{\infty} \tilde{F}(\omega) \ e^{- \, 2 \pi i x \omega} \ d \omega ,
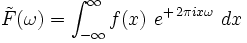\tilde{F}(\omega) = \int_{-\infty}^{\infty} f(x) \ e^{+ \, 2 \pi i x \omega} \ dx ,

alors la formule sommatoire de Poisson se réécrit (avec 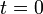t=0\, et a=1\,) :

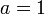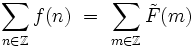\sum_{n \in \mathbb{Z}} f(n) \ = \ \sum_{m \in \mathbb{Z}} \tilde{F}(m) .

Sur les conditions de convergence

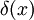Une façon pratique de passer outre les conditions de régularité imposées à la fonction f\, est de se placer dans le contexte plus général de la théorie des distributions. Si on note \delta (x)\, la distribution de Dirac alors si on introduit la distribution suivante :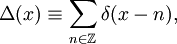

\Delta (x) \equiv \sum_{n\in\mathbb{Z}}\delta (x-n),

une façon élégante de reformuler la sommation est de dire que 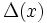\Delta (x)\, est sa propre transformée de Fourier.

Applications de la resommation de Poisson

Les exemples les plus élémentaires de cette formule permettent de déterminer des sommes simples d'entiers :

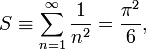
S \equiv \sum_{n=1}^{\infty} \frac{1}{n^{2}} = \frac{\pi^{2}}{6},

ou bien encore :

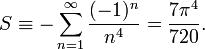
S \equiv -\sum_{n=1}^\infty \frac{(-1)^n}{n^4}= \frac{7\pi^4}{720}.

En les convertissant en séries géométriques qui peuvent être sommées exactement.

De façon générale, la resommation de Poisson est utile dans la mesure ou une série qui converge lentement dans l'espace direct peut être transformée en une série convergeant beaucoup plus vite dans l'espace de Fourier(si on prend l'exemple de fonctions gaussiennes, une gaussienne de grande variance dans l'espace direct est convertie en une gaussienne de variance petite dans l'espace de Fourier). C'est l'idée essentielle qui sous-tend la sommation d'Ewald.

Interprétation géométrique

Définitions

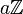Le cercle plat, ou tore T à une dimension, est une courbe compacte de courbure nulle qui peut se représenter comme l'espace quotient de la droite euclidienne \mathbb{R} par un sous-groupe discret a \mathbb{Z} du groupe des isométries :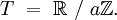

T \ = \ \mathbb{R} \ / \ a \mathbb{Z}.

Géodésiques périodiques

Les géodésiques périodiques du tore plat ont pour longueurs :

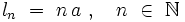
l_n \ = \ n \, a \ , \quad n \ \in \ \mathbb{N}

.

Spectre de l'opérateur de Laplace-Beltrami

Considérons l'opérateur de Laplace sur T :

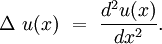
\Delta \ u(x) \ = \ \frac{d^2 u(x)}{d x^2}.

Cherchons en particulier ses valeurs propres λn, solution de l'équation aux valeurs propres :

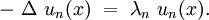
- \ \Delta \ u_n(x) \ = \ \lambda_n \ u_n(x).

où les fonctions propres sont dans 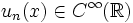u_n(x) \in C^{\infty}(\mathbb{R}) et vérifient la condition de périodicité :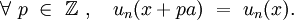

\forall \ p \ \in \ \mathbb{Z} \ , \quad u_n( x + p a ) \ = \ u_n(x).

Ces valeurs propres forment une suite dénombrable :

\lambda_n \ = \ \frac{4 \pi^2 n^2}{a^2} \ , \quad n \ \in \ \mathbb{N},

qu'on peut ranger par ordre croissant :

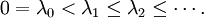
0 = \lambda_0 < \lambda_1 \leq \lambda_2 \leq \cdots .

Généralisations

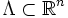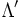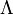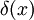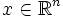On peut facilement formuler une généralisation de cette formule en dimension n\,. Étant donné un réseau \Lambda\subset\mathbb{R}^n\, alors on peut définir le réseau dual \Lambda'\, (comme formes dans l'espace vectoriel dual à valeur entière sur \Lambda\, ou via la dualité de Pontryagin). Alors si on considère la distribution de dirac multidimensionnelle qu'on note encore \delta (x)\, avec x\in\mathbb{R}^n\, on peut définir la distribution

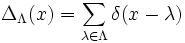\Delta_{\Lambda}(x)=\sum_{\lambda\in\Lambda}\delta (x-\lambda) \,.

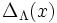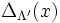Cette fois-ci on obtient une formule sommatoire de Poisson en remarquant que la transformée de Fourier de \Delta_{\Lambda} (x)\, est \Delta_{\Lambda'} (x)\, (en considérant une normalisation appropriée de la transformée de Fourier).

Cette formule est souvent utilisée dans la théorie des fonctions theta. En théorie des nombres on peut généraliser encore cette formule au cas d'un groupe abélien localement compact. En analyse harmonique non-commutative cette idée est poussée encore plus loin et aboutit à la formule des traces de Selberg et prend un caractère beaucoup plus profond.

Un cas particulier est celui des groupes abéliens finis, la formule sommatoire de poisson s'applique simplement (cf Analyse harmonique sur un groupe abélien fini) et possède de nombreuses applications à la fois théoriques en arithmétique et appliquées par exemple en théorie des codes et en cryptographie (cf fonction booléenne).

Articles connexes

Bibliographie

  • Matthew R. Watkins ; page personnelle sur les liens entre la théorie des nombres et la physique théorique.
  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Formule sommatoire de Poisson ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule de sommation de Poisson de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Sommation d'Ewald — La sommation d Ewald (ou parfois somme d Ewald) est une méthode de calcul des énergies d interaction de systèmes périodiques (et particulier des cristaux), et tout particulièrement les énergies électrostatiques. La sommation d Ewald est un cas… …   Wikipédia en Français

  • Formule Sommatoire De Poisson — Pour les articles homonymes, voir Poisson (homonymie). La formule sommatoire de Poisson, parfois appelée resommation de Poisson, établit une relation entre le spectre de l opérateur de Laplace Beltrami sur le cercle et les longueurs des… …   Wikipédia en Français

  • Formule sommatoire de poisson — Pour les articles homonymes, voir Poisson (homonymie). La formule sommatoire de Poisson, parfois appelée resommation de Poisson, établit une relation entre le spectre de l opérateur de Laplace Beltrami sur le cercle et les longueurs des… …   Wikipédia en Français

  • Formule sommatoire de Poisson — Pour les articles homonymes, voir Poisson (homonymie). La formule sommatoire de Poisson (parfois appelée resommation de Poisson) est une identité entre deux sommes infinies, la première construite avec une fonction f, la seconde avec sa… …   Wikipédia en Français

  • Resommation de Poisson — Formule sommatoire de Poisson Pour les articles homonymes, voir Poisson (homonymie). La formule sommatoire de Poisson, parfois appelée resommation de Poisson, établit une relation entre le spectre de l opérateur de Laplace Beltrami sur le cercle… …   Wikipédia en Français

  • Maillage particulier d'Ewald — Sommation d Ewald La sommation d Ewald (ou parfois somme d Ewald) est une méthode de calcul des énergies d interaction de systèmes périodiques (et particulier des cristaux), et tout particulièrement les énergies électrostatiques. La sommation d… …   Wikipédia en Français

  • Somme d'Ewald — Sommation d Ewald La sommation d Ewald (ou parfois somme d Ewald) est une méthode de calcul des énergies d interaction de systèmes périodiques (et particulier des cristaux), et tout particulièrement les énergies électrostatiques. La sommation d… …   Wikipédia en Français

  • Forme Modulaire — En mathématiques, une forme modulaire est une fonction analytique sur le demi plan de Poincaré satisfaisant à une certaine sorte d équation fonctionnelle et de condition de croissance. La théorie des formes modulaires par conséquent est dans la… …   Wikipédia en Français

  • Forme modulaire — En mathématiques, une forme modulaire est une fonction analytique sur le demi plan de Poincaré satisfaisant à une certaine sorte d équation fonctionnelle et de condition de croissance. La théorie des formes modulaires par conséquent est dans la… …   Wikipédia en Français

  • Transformée de Fourier — Joseph Fourier En analyse, la transformation de Fourier est un analogue de la théorie des séries de Fourier pour les fonctions non périodiques, et permet de leur associer un spectre en fréquences. On cherche ensuite à obtenir l expression de la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”