- Formalisme Complexe
-
Formalisme complexe
Soit une grandeur physique x définie par :
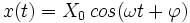
 est donc une fonction sinusoïdale du temps.
est donc une fonction sinusoïdale du temps.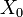 est l'amplitude de
est l'amplitude de 
 est la phase de
est la phase de  .
.
A
 , on associe une valeur complexe notée
, on associe une valeur complexe notée 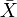 , telle que
, telle que 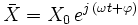
Donc
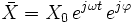
On pose
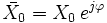
On a alors :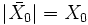 : c'est l'amplitude de
: c'est l'amplitude de 
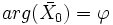 : c'est la phase de
: c'est la phase de  .
.
Opérations mathématiques
- La dérivation :
Lorsque l'on dérive la grandeur
 par rapport au temps, on obtient :
par rapport au temps, on obtient :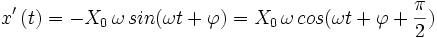
A
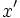 , on associe une valeur complexe notée
, on associe une valeur complexe notée 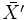
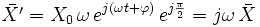 car
car 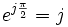 et
et 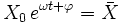 .
.Dériver une grandeur
 par rapport au temps, revient à multiplier
par rapport au temps, revient à multiplier 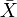 par
par 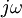 en formalisme complexe.
en formalisme complexe.- L'intégration :
On montre de la même manière qu'intégrer une grandeur x par rapport au temps, revient à diviser celle-ci par jω.
Catégorie : Équation aux dérivées partielles
Wikimedia Foundation. 2010.
