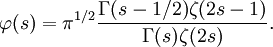Fonction zeta de Selberg

Fonction zeta de Selberg

Fonction zêta de Selberg

Pour chaque surface hyperbolique de volume fini, on peut définir une fonction zêta de Selberg. C'est une fonction méromorphe d'une variable complexe. Elle est définie par le biais des géodésiques fermées sur la surface.

Les zéros et les pôles de la fonction zêta de Selberg Z(s) admettent une description en termes de données spectrales de la surface.

Les zéros sont aux points suivants :

  1. Pour chaque forme parabolique pour la valeur propre s0(1 − s0), il y a un zéro au point s0. L'ordre du zéro est la dimension de l'espace propre correspondant. (Une forme parabolique est une fonction propre de l'opérateur de Laplace-Beltrami dont le développement de Fourier est sans terme constant.)
  2. La fonction zêta a aussi un zéro en chaque pôle du déterminant de la matrice de scattering, φ(s). L'ordre du zéro est égal à l'ordre du pôle correspondant.

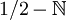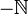La fonction zêta a aussi des pôles en 1/2 - \mathbb{N} , et peut avoir des zéros ou des pôles en les points de - \mathbb{N} .

la fonction zêta de Selberg zêta pour le groupe modulaire

Dans le cas où la surface est 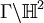\Gamma \backslash \mathbb{H}^2 , où Γ est le groupe modulaire, la fonction zêta de Selberg est particulièrement intéressante. Elle est en effet liée très fortement à la fonction zêta de Riemann.

Dans ce cas, la matrice scattering est donnée par

\varphi(s) = \pi^{1/2} \frac{ \Gamma(s-1/2) \zeta(2s-1) }{ \Gamma(s) \zeta(2s) }.

On voit que si la fonction zêta de Riemann a un zéro en s0, alors la matrice scattering a un pôle en s0 / 2, donc la fonction zêta de Selberg a un zéro en s0 / 2.

Bibliographie

  • Hejhal, D. A. The Selberg trace formula for PSL(2,R). Vol. 2, Springer-Verlag, Berlin, 1983.
  • Iwaniec, H. Spectral methods of automorphic forms, American Mathematical Society, second edition, 2002.
  • Venkov, A. B. Spectral theory of automorphic functions. Proc. Steklov. Inst. Math, 1982.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction z%C3%AAta de Selberg ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction zeta de Selberg de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Fonction Zeta De Selberg — Fonction zêta de Selberg Pour chaque surface hyperbolique de volume fini, on peut définir une fonction zêta de Selberg. C est une fonction méromorphe d une variable complexe. Elle est définie par le biais des géodésiques fermées sur la surface.… …   Wikipédia en Français

  • Fonction Zeta de Selberg — Fonction zêta de Selberg Pour chaque surface hyperbolique de volume fini, on peut définir une fonction zêta de Selberg. C est une fonction méromorphe d une variable complexe. Elle est définie par le biais des géodésiques fermées sur la surface.… …   Wikipédia en Français

  • Fonction zeta de selberg — Fonction zêta de Selberg Pour chaque surface hyperbolique de volume fini, on peut définir une fonction zêta de Selberg. C est une fonction méromorphe d une variable complexe. Elle est définie par le biais des géodésiques fermées sur la surface.… …   Wikipédia en Français

  • Fonction zêta de Selberg — Pour chaque surface hyperbolique de volume fini, on peut définir une fonction zêta de Selberg. C est une fonction méromorphe d une variable complexe. Elle est définie par le biais des géodésiques fermées sur la surface. Les zéros et les pôles de… …   Wikipédia en Français

  • Fonction Zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zêta — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction zêta de… …   Wikipédia en Français

  • Fonction Zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction Zêta De Riemann — En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des nombres premiers. Elle est… …   Wikipédia en Français

  • Fonction zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”