Fonction symetrique

Fonction symetrique

Polynôme symétrique

En mathématiques, un polynôme symétrique est un polynôme en plusieurs indéterminées, invariant par permutation de ses indéterminées. Ils jouent notamment un rôle dans les relations entre coefficients et racines.

Définition

Dans un espace K[T_1,\dots,T_n] de polynômes à plusieurs indéterminées, un polynôme P(T1,...,Tn) est dit symétrique si pour toute permutation s de l'ensemble d'indices [1,n], l'égalité suivante est vérifiée : 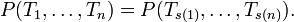P(T_1,\dots,T_n)=P(T_{s(1)},\dots,T_{s(n)}). Pour n=1, tout polynôme est symétrique. Pour n=2, le polynôme T1+T2 est symétrique alors que le polynôme T1-T2 ne l'est pas, du moins en caractéristique différente de 2 (puisque la transposition des indices transforme le polynôme en son opposé).

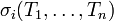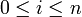Les polynômes symétriques forment une sous-algèbre de K[T_1,\dots,T_n]. Une famille génératrice est donnée par les polynômes symétriques élémentaires : ce sont les polynômes \sigma_i(T_1,\dots,T_n), pour 0\leq i\leq n définis par :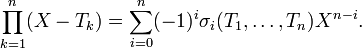

\prod_{k=1}^n (X-T_k)=\sum_{i=0}^n(-1)^i\sigma_i(T_1,\dots,T_n)X^{n-i}.

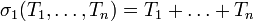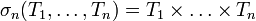En particulier, \sigma_1(T_1,\dots,T_n)=T_1+\dots+T_n, et \sigma_n(T_1,\dots,T_n)=T_1\times\dots\times T_n. Plus précisément, le morphisme d'algèbre défini par :

\begin{array} {ccc} K[X_1,\dots X_n] & \to & K[\sigma_1(T_1,\dots,T_n),\dots,\sigma_n(T_1,\dots,T_n)]\\ X_i & \mapsto & \sigma_i(T_1,\dots,T_n) \end{array}

est un isomorphisme à valeurs dans l'algèbre des polynômes symétriques[1]. Un autre système de générateurs célèbre, lié au précédent, est constitué des sommes de Newton.

Dans le contexte de la théorie des polynômes à une indéterminée, si un tel polynôme admet une factorisation 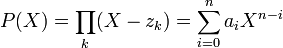P(X)=\prod_k(X-z_k)=\sum_{i=0}^n a_iX^{n-i} en facteurs de degré 1, alors les coefficients du polynôme P sont donnés comme fonctions symétriques des racines zi, c'est-à-dire :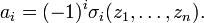

a_i=(-1)^i\sigma_i(z_1,\dots,z_n).

Notes et références

  1. ↑ voir par exemple Algèbre commutative de Rémi Goblot, théorème 7.3. Dunod.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Polyn%C3%B4me sym%C3%A9trique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction symetrique de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • fonction symétrique — simetrinė funkcija statusas T sritis fizika atitikmenys: angl. symmetric function vok. symmetrische Funktion, f rus. симметрическая функция, f pranc. fonction symétrique, f …   Fizikos terminų žodynas

  • Fonction Symétrique — Polynôme symétrique En mathématiques, un polynôme symétrique est un polynôme en plusieurs indéterminées, invariant par permutation de ses indéterminées. Ils jouent notamment un rôle dans les relations entre coefficients et racines. Définition… …   Wikipédia en Français

  • Fonction symétrique — Polynôme symétrique En mathématiques, un polynôme symétrique est un polynôme en plusieurs indéterminées, invariant par permutation de ses indéterminées. Ils jouent notamment un rôle dans les relations entre coefficients et racines. Définition… …   Wikipédia en Français

  • Application ou fonction symétrique — ● Application ou fonction symétrique application f de l ensemble En (n ∊ N) dans l ensemble F telle que la valeur de la fonction ne change pas si on permute les variables x1, x2, …,xn …   Encyclopédie Universelle

  • symétrique — [ simetrik ] adj. • symmétrique 1530; de symétrie 1 ♦ Vx ou littér. Qui a de la symétrie (I). ⇒ régulier. Dans ces lettres, « tout est mesquin, symétrique et rabougri » (Gautier). 2 ♦ Cour. Qui présente une symétrie, est en rapport de symétrie… …   Encyclopédie Universelle

  • symétrique — (si mé tri k ) adj. 1°   Qui a de la symétrie. Arrangement symétrique. Phrases symétriques. •   Les vieilles même au marcher symétrique Des ans tardifs ont oublié le poids, GRESSET Ver vert, III. •   L ordonnance de la Critique de la raison… …   Dictionnaire de la Langue Française d'Émile Littré

  • Fonction aléatoire intrinsèque — Une fonction aléatoire intrinsèque d ordre k (en abrégé FAI k) est une classe de fonction aléatoire respectant certaines conditions. Cette propriété étend celle de fonction aléatoire intrinsèque. Une fonction aléatoire intrinsèque stricte est une …   Wikipédia en Français

  • Fonction de Dawson — La fonction de Dawson, F(x), près de l origine …   Wikipédia en Français

  • Fonction Trigonométrique — Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u …   Wikipédia en Français

  • Fonction arcsin — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”