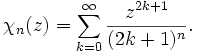Fonction chi de legendre
- Fonction chi de legendre
-
Fonction chi de Legendre
En mathématiques, la fonction chi de Legendre est définie par
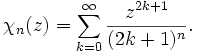
La transformée discrète de Fourier de la fonction chi de Legendre en respectant l'ordre n est la fonction zeta d'Hurwitz (Cvijovic).
La fonction chi de Legendre est un cas particulier de la fonction transcendante de Lerch, et est donnée par
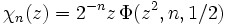 .
.
Publication en langue anglaise
- Djurdje Cvijovic and Jacek Klinowski. Math. Comp. 68 (1999), 1623-1630, 1999. (abstract)
 Portail des mathématiques
Portail des mathématiques
Catégorie : Fonction remarquable
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Fonction chi de legendre de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fonction Chi De Legendre — En mathématiques, la fonction chi de Legendre est définie par La transformée discrète de Fourier de la fonction chi de Legendre en respectant l ordre n est la fonction zeta d Hurwitz (Cvijovic). La fonction chi de Legendre est un cas particulier… … Wikipédia en Français
Fonction chi de Legendre — En mathématiques, la fonction chi de Legendre est définie par La transformée de Fourier discrète de la fonction chi de Legendre en respectant l ordre n est la fonction zêta de Hurwitz (Cvijovic). La fonction chi de Legendre est un cas particulier … Wikipédia en Français
Fonction Polylogarithme — La fonction polylogarithme (aussi connue sous le nom de fonction de Jonquière) est une fonction remarquable et peut être définie pour tout s et |z|<1 par : Le paramètre s et l argument z sont pris sur l ensemble , l ensemble des nombres… … Wikipédia en Français
Fonction Zeta D'Hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction Zeta d'Hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction zeta d'Hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction zeta d'hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction zêta d'Hurwitz — En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre complexe q qui n est pas… … Wikipédia en Français
Fonction Zeta De Lerch — Fonction zêta de Lerch En mathématiques, la fonction zêta de Lerch est une fonction spéciale qui généralise la fonction zêta d Hurwitz et le polylogarithme. Elle est donnée par La fonction zêta de Lerch est reliée à la fonction transcendante de… … Wikipédia en Français
Fonction zeta de Lerch — Fonction zêta de Lerch En mathématiques, la fonction zêta de Lerch est une fonction spéciale qui généralise la fonction zêta d Hurwitz et le polylogarithme. Elle est donnée par La fonction zêta de Lerch est reliée à la fonction transcendante de… … Wikipédia en Français
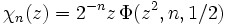 .
.