- Fonction Sous-Modulaire
-
Fonction sous-modulaire
Les fonctions sous-modulaires jouent un rôle important en optimisation combinatoire.
Dans ce contexte il s'agit de sous-modularité sur des fonctions d'ensemble, c'est-à-dire des fonctions de l'ensemble des parties d'un ensemble (que l'on peut supposer fini) dans l'ensemble des réels. (Le terme « sous-modulaire » s'applique aussi pour les fonctions continues.)
Donc, soient E un ensemble et f une fonction qui à tout sous-ensemble X de E associe un réel f(X), on dit que f est sous-modulaire si l'inégalité suivante est vérifiée pour tout sous-ensemble X et Y de E
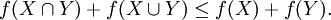
(On peut définir la sous-modularité à l'aide d'autres inégalités équivalentes.)
Des exemples de fonctions sous-modulaires sont les fonctions de rang des matroïdes, ou en théorie des graphes la fonction qui associe à tout sous-ensemble de sommets d'un graphe la cardinalité de sa coupe. On trouve aussi des exemples liés à des concepts concernant l'entropie ou les probabilités.
Le résultat crucial des fonctions d'ensemble sous-modulaires est algorithmique:
- On peut minimiser une fonction sous-modulaire en temps polynomial.
On pourra consulter à ce propos l'article de Lex Schrijver, "A combinatorial algorithm minimizing submodular functions in strongly polynomial time", Journal of Combinatorial Theory Series B, Volume 80 , Issue 2 (November 2000) Pages: 346 - 355 (ISSN:0095-8956).
- Portail des mathématiques
Catégories : Optimisation | Optimisation combinatoire
Wikimedia Foundation. 2010.
