- Flocon de neige de Von Koch
-
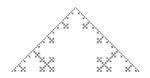
Flocon de von Koch
Pour les articles homonymes, voir Koch.Le flocon de Koch est l'une des premières courbes fractales à avoir été décrite (bien avant l'invention du terme « fractal(e) »).
Elle apparaît en 1906 dans un article intitulé « Une méthode géométrique élémentaire pour l'étude de certaines questions de la théorie des courbes planes » et écrit par le mathématicien suédois Helge von Koch (1870 - 1924)[1].
Sommaire
Courbe de Koch
les 4 premières étapes de la construction
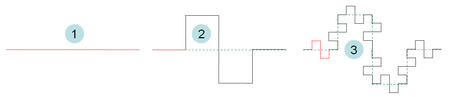
les 6 premières courbes successives en animationOn peut la créer à partir d'un segment de droite, en modifiant récursivement chaque segment de droite de la façon suivante :
- on divise le segment de droite en trois segments de longueurs égales,
- on construit un triangle équilatéral ayant pour base le segment médian de la première étape,
- on supprime le segment de droite qui était la base du triangle de la deuxième étape.
Au bout de ces trois étapes, l'objet résultant a une forme similaire à une coupe transversale d'un chapeau de sorcière.
La courbe de Koch est la limite des courbes obtenues, lorsqu'on répète indéfiniment les étapes mentionnées ci-dessus.
Une extension de la notion de dimension permet d'attribuer à la courbe de Koch une dimension fractale[2] (non entière) dont la valeur est
.
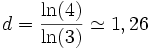La courbe de Koch a une longueur infinie parce qu'à chaque fois qu'on applique les modifications ci-dessus sur chaque segment de droite, la longueur totale augmente d'un tiers.
La surface délimitée par la courbe est cependant finie (car elle est contenue dans le demi-cercle dont le diamètre est le segment initial). Si on a choisi l'unité d'aire de telle sorte que le triangle construit à la première itération soit d'aire 1, alors l'aire de chacun des quatre triangles construits lors de la seconde itération est 1/9 : on a donc augmenté l'aire totale de 4/9. Pour l'itération n, on ajoute
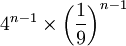. La surface totale s'obtient finalement en sommant une série géométrique :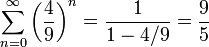
Flocon de Koch
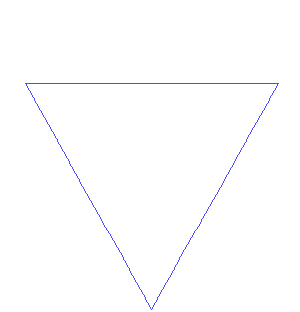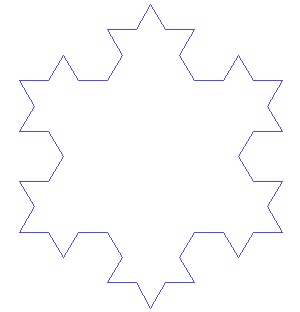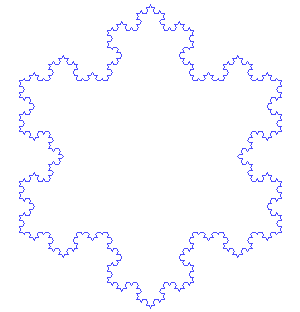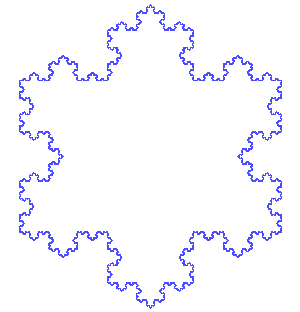Création du flocon de KochLe flocon de Koch s'obtient de la même façon que la fractale précédente, en partant d'un triangle équilatéral au lieu d'un segment de droite, et en effectuant les modifications en orientant les triangles vers l'extérieur. On peut aussi partir d'un hexagone, et opérer en orientant les triangles vers l'intérieur. Dans les deux cas, après quelques itérations on obtient une forme évoquant un flocon de neige régulier.
Comme la courbe, le flocon de Koch est de longueur infinie et délimite une aire finie égale au 8/5 de l'aire du triangle initial.
Variantes de la courbe de von Koch
Suivant le concept de von Koch, plusieurs variantes ont été conçues, en considérant des angles droits (Quadratique), d'autres angles (fractale de Cesaro) ou des extensions dans les dimensions supérieures (sphereflake, surface de Koch).
Variante Illustration Construction 1D & angle=85° 
Fractale Cesaro.La fractale Cesaro est une généralisation de la courbe de Koch avec un angle compris entre 60° et 90° (ici 85°). 1D & 90° 
Courbe quadratique de Koch (type 1)
Les 2 premières itérations.1D & 90° 
Courbe quadratique de Koch (type 2)
Les deux premières itérations. Sa dimension fractale égale 1,5, soit à mi-chemin entre la dimension 1 et la dimension 2. Cette propriété en fait une courbe très utilisée dans l'étude des propriétés physiques des objets fractals (Cf Sapoval).2D & triangles 
Surface de von Koch
Les 2 premières itérations. Extension naturelle à 2 dimensions de la courbe de von Koch .2D & 90° 
Surface quadratique de Koch (type 1)
Les trois premières étapes.2D & 90° 
Surface quadratique de Koch (type 2)
Les trois premières étapes.2D & spheres Eric Haines a développé la fractale sphereflake, extension du flocon de Koch, construite à base de sphères. Notes et références
- ↑ (en) Biographie de von Koch
- ↑ Une démonstration figure dans Les fractales. Tangente HS n° 18 page 26
Voir aussi
Liens externes
Portail de la géométrie
Catégorie : Fractale
Wikimedia Foundation. 2010.
