Fenêtre de Viviani
- Fenêtre de Viviani
-
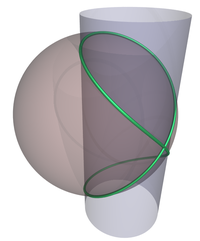
Vue en perspective de la fenêtre de Viviani
La fenêtre de Viviani est une courbe algébrique gauche, et une courbe fermée, définie comme l'intersection d'une sphère et d'un cylindre circulaire de rayon moitié de celui de la sphère, et passant par le centre de la sphère.
Vincenzo Viviani proposa en 1692 le problème d'architecture suivant[1] : il s'agissait de percer une coupole hémisphérique de quatre fenêtres de telle façon que la surface restante de la coupole soit quarrable. John Wallis, Gottfried Wilhelm Leibniz et Jean Bernoulli étudièrent naturellement le cas simple de fenêtres circulaires, et durent étudier la courbe intersection du cylindre et de l'hémisphère, donnant à cette courbe le nom de « fenêtre de Viviani »[2].
L'architecte Paul Andreu a dessiné le dôme du Musée maritime d'Ōsaka, en disposant les armatures selon un réseau de courbes de Viviani parallèles.
Équations de la fenêtre de Viviani
Cette section est vide,
insuffisamment détaillée ou incomplète.
Votre aide est la bienvenue !
On a les représentations suivantes[3] (pour une sphère de rayon R) :
- Système d’équations cartésiennes : x2 + y2 + z2 = R2 et x2 + y2 = Rx.
- Paramétrisation cartésienne : x = Rcos 2u, y = Rcos usin u et z = Rsin u.
Notes et références

Le dôme du musée maritime d'
Osaka.
Notes
Références
- Michel Chasles, Aperçu historique sur l'origine et le développement des méthodes en géométrie (1837), impr. Hayez, Bruxelles
- Michel Serres, Le système de Leibnitz et ses modèles mathématiques (1968, rééd. 2007) éd. PUF, coll. Épiméthée (ISBN 2130433898)
- (fr) Denis Lanier, « Leibniz, la nouvelle analyse et la géométrie ou enquête sur la fenêtre de Viviani » sur NUMDAM, Cahiers du séminaire d'histoire des mathématiques, vol. 8, 1987, p. 203-227. Consulté le 28 oct. 2007
Lien externe
La fenêtre de Viviani sur Mathcurve
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Fenêtre de Viviani de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fenetre de Viviani — Fenêtre de Viviani Pour les articles homonymes, voir Fenêtre (homonymie). La fenêtre de Viviani est une courbe algébrique gauche, et une courbe fermée, définie comme l intersection d une sphère et d un cylindre circulaire de rayon moitié de celui … Wikipédia en Français
Fenêtre De Viviani — Pour les articles homonymes, voir Fenêtre (homonymie). La fenêtre de Viviani est une courbe algébrique gauche, et une courbe fermée, définie comme l intersection d une sphère et d un cylindre circulaire de rayon moitié de celui de la sphère, et… … Wikipédia en Français
Fenêtre de viviani — Pour les articles homonymes, voir Fenêtre (homonymie). La fenêtre de Viviani est une courbe algébrique gauche, et une courbe fermée, définie comme l intersection d une sphère et d un cylindre circulaire de rayon moitié de celui de la sphère, et… … Wikipédia en Français
Fenetre (homonymie) — Fenêtre (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Fenêtre (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Fenêtre (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Fenêtre (homonymie) », sur le Wiktionnaire (dictionnaire universel) Le mot fenêtre est employé dans… … Wikipédia en Français
Vincenzo Viviani — Pour les articles homonymes, voir Viviani. Vincenzo Viviani … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Besace — En mathématiques, la besace est une courbe qui a été étudiée et nommée ainsi par Gabriel Cramer en 1750. Équations Équation cartésienne : . Paramétrisation cartésienne : Aire totale … Wikipédia en Français


