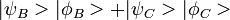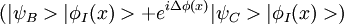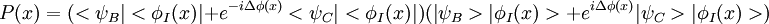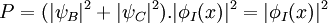Expérience de Marlan Scully

Cet article fait partie de la série Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

L’expérience de la gomme quantique à choix retardé^[1] est une expérience de mécanique quantique qui constitue une extension de celle d'Alain Aspect et des fentes d'Young en y introduisant ce qui semble être une rétroaction implicite dans le temps. Elle a été menée, en 1999, par Marlan Scully, B.-G. Englert, et H. Walther, d'où le nom parfois employé d'expérience ESW, et avait été proposé par Scully and Drühl dès 1982.

Schématiquement, deux dispositifs similaires aux fentes d'Young sont installés en cascade.

On sait que l'incertitude quantique concernant le passage (éventuel !) de particules par l'une ou l'autre fente

• n'est levable que par un processus de détection,
• et subsiste en l'absence de celle-ci non seulement en tant que connaissance de l'expérimentateur, mais bien en tant qu'état du système.

L'idée de Marlan Scully est de ne décider l'intervention de cet observateur qu'au dernier moment, alors que la particule^[2] a déjà franchi la première série de fentes.

Les équations de la mécanique quantique imposent à la particule d'avoir vérifié lors du premier passage des conditions qui ne sont pourtant stipulées que postérieurement, par intervention ultérieure du détecteur ou non. En d'autres termes, cette intervention du détecteur semble modifier le passé de la particule.

L'observation confirme pour le moment ce résultat prévu, mais Marlan Scully ne se prononce pas encore sur les enseignements que l'on peut ou non en tirer. John Wheeler s'est montré parfois moins réservé et a tenu à ce sujet des propos controversés sur la modification du passé par des processus d'observation (à moins, selon une autre interprétation du même phénomène, qu'il ne s'agisse d'une définition du présent par le résultat de l'observation de phénomènes passés — voir l'interprétation d'Everett).

Sommaire 1 Description de l'expérience 2 Figures d'interférences 3 Enjeux et interprétations 4 Enjeux et interprétations - complément 5 Voir aussi 6 Notes 7 Liens externes

Description de l'expérience

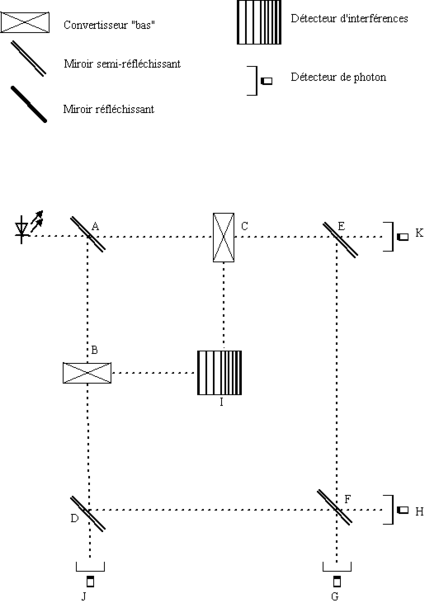
L'expérience est plus simple qu'il n'y paraît. Le dispositif va être décrit progressivement, afin de bien faire apparaître les idées derrière chaque élément de l'expérience.

Décrivons d'abord la première partie du dispositif : si nous remplaçons les appareils B et C par de simples miroirs, nous nous retrouvons avec une variante de l'expérience des fentes de Young : le miroir semi-réfléchissant A provoque une interférence « du photon avec lui-même » et provoque une figure d'interférence en I. Il est important de bien comprendre l'expérience de Young avant de tenter de comprendre celle-ci.

En fait, en B et en C, sont placés des « convertisseurs bas ». Un « convertisseur bas » est un appareil qui, à partir d'un photon en entrée, crée deux photons en sortie, corrélés, et de longueur d'onde double par rapport au photon en entrée. Étant corrélés, toute mesure effectuée sur un des deux photons de sortie nous renseigne sur l'état de l'autre photon. Par définition, un des deux photons en sortie sera appelé « photon signal » et l'autre « photon témoin ». Il est important aussi de souligner que le « convertisseur bas » ne détruit pas l'état quantique du photon : il n'y a pas de « mesure » et l'état des deux photons en sortie respecte l'état de superposition du photon en entrée. Cependant, les photons corrélés par les convertisseurs bas ne génèrent pas de figure d'interférences immédiatement visible en I (voir paragraphe figure d'interférences).

Maintenant, imaginons qu'il n'y ait pas de miroir semi-réfléchissant en D et en E. Ne pourrait-on pas détecter par quel chemin ( « par B » ou « par C ») est passé le photon initialement émis ? Si le détecteur J se déclenche, c'est que le photon est passé par B, si c'est K, c'est que le photon est passé par C. Les « photons signaux » se comportant de la même manière que s'il y avait des miroirs en B ou en C, la figure d'interférence ne devrait-elle pas apparaître, tout en nous renseignant sur le chemin pris par le photon ? (ce serait en contradiction avec l'expérience de Young)

En fait, non. La « mesure » effectuée par un des détecteur J ou K détruit l'état quantique des photons « signal » et « témoin » (ceux-ci étant quantiquement corrélés, voir paradoxe EPR), et aucune figure d'interférence n'apparaît en I. Nous retrouvons bien les résultats de l'expérience de Young.

Maintenant, considérons le dispositif complet, représenté par la figure. Le photon témoin a une chance sur deux d'être réfléchi par le miroir D ou E. Dans ce cas il arrive en F et il n'y a alors plus moyen de savoir si le photon est passé par B ou par C. En effet, que le photon vienne de E ou de D, il a dans les deux cas une chance sur deux d'être détecté en H ou en G. Donc la détection en H ou G ne permet pas de savoir d'où vient le photon. Ce miroir F est la « gomme quantique » imaginée par Sculley : il détruit l'information permettant de savoir par quel chemin est passé le photon.

Cependant, si au lieu d'avoir été réfléchi par D ou E, le photon témoin a été détecté par J ou K, alors il est possible de savoir le chemin emprunté par le photon, et le photon signal correspondant enregistré en I ne contribue pas à faire une figure d'interférence. Les miroirs D et E "tirent au sort" - en quelque sorte - le destin du photon témoin : une chance sur deux de devenir un photon dont on connaît le chemin, une chance sur deux de devenir un photon dont le chemin est indéterminé.

Or, la distance BD (et a fortiori BF) peut être très supérieure à la distance BI, et de même pour respectivement CE/CF et CI. Et c'est le cas dans cette expérience. Donc, quand le photon signal vient impressionner la plaque photographique en I, le photon témoin n'a pas encore atteint D ou E, et encore moins F. C'est le "choix retardé" dont il est question dans l'expérience. Le résultat enregistré en I est donc fixé avant que le photon témoin ait été détecté en J/K, ou en G/H.

Au moment où le photon signal impressionne I, le chemin du photon témoin est encore indéterminé. La figure en I devrait donc s'organiser systématiquement en figure d'interférence. Pourtant, un photon témoin sur deux en moyenne sera détecté en J/K, et les photons signaux correspondant ne doivent pas s'organiser en figure d'interférence (puisque on connaît le chemin emprunté). Comment le photon signal "sait-il" que le photon témoin sera détecté en J/K ou non ? Telle est la question fondamentale de cette expérience.

Expérimentalement on constate qu'il n'y a jamais d'erreur : les photons signaux dont les photons témoins sont détectés en J/K ne s'organisent pas en figure d'interférence, les photons signaux dont les photons témoins sont détectés en G/H s'organisent en figure d'interférence (voir section suivante).

Figures d'interférences

Lorsque les impacts de photons sont matérialisés en I, on ne voit qu'un brouillard sans signification. C'est la corrélation entre chaque impact et le capteur qui permet de faire apparaître les franges d'interférence. Ici, les photons sont colorés en fonction du capteur qui les a reçus. Lorsque l'on sépare l'image en quatre, on voit nettement apparaître les figures d'interférence pour les photons détectés en G et H.

À noter que les deux figures 3. et 4. sont complémentaires, en opposition de phase. L'addition de ces deux figures donne une figure similaire à la figure 2. ou 1. Cela explique la nécessité de recevoir des corrélations pour faire apparaître les figures d'interférence. Sans corrélations, il n'y a aucun moyen de distinguer le cas 3.+4. du cas 5.+6.

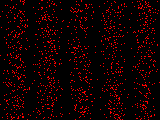
1. La figure telle qu'elle est reçue en I	2. Corrélation entre les impacts et les 4 détecteurs	3. Photons corrélés avec le détecteur G
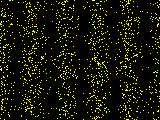
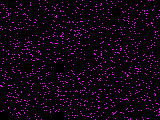
4. Photons corrélés avec le détecteur H	5. Photons corrélés avec le détecteur J	6. Photons corrélés avec le détecteur K

Note : Ces images sont des simulations

Enjeux et interprétations

L'aspect le plus spectaculaire de cette expérience est l'interprétation que l'on fait a posteriori de la figure d'interférence en I. Tant que l'on n'a pas reçu les informations de corrélation en provenance des détecteurs G et H (qui peuvent être, disons, à cent années-lumière !), il est impossible de déterminer si la figure en I contient ou non une figure d'interférence.

Si cela était possible, cela voudrait dire que l'on pourrait recevoir des messages du futur ! Par exemple, si, en même temps que le photon, on émettait un message en destination d'un physicien (à cent années-lumière de là) lui demandant si, par exemple, la théorie des cordes est exacte ou non, et de remplacer les miroirs D/E par des miroirs parfaitement réfléchissants si oui, et de les enlever si non, alors il serait possible de savoir immédiatement si la théorie des cordes est valable ou non en décryptant une figure d'interférence en I.

On pourrait alors véritablement parler de « rétroaction en provenance du futur ». Mais tel n'est pas le cas. Certaines interprétation hâtives et sensationnalistes laissent penser cela, mais on voit clairement que ce n'est pas aussi simple.

En effet, force est de constater que la figure en I contient une information indécryptable qui dépend de quelque chose qui se passe dans le futur. Mais elle ne peut être décryptée qu'avec des informations « classiques » (sur cette chose) qui ne peuvent être connues, au plus tôt, que dans un délai qui annule le bénéfice de la rétroaction temporelle (par exemple, dans le cas de l'interrogation d'un physicien à 100 années-lumière, on ne connaîtrait la réponse à la question que - au mieux - 100 ans plus tard).

En fait, ce résultat, bien que spectaculaire, n'est pas plus surprenant (ni moins) que les résultats déjà connus des expériences EPR. En effet, dans ces expériences, l'effondrement d'un côté du dispositif provoque immédiatement l'effondrement de l'autre côté, aussi éloigné soit-il. Mais on ne peut s'en rendre compte qu'avec l'envoi d'une information classique (évitant de pouvoir communiquer à une vitesse supérieure à celle de la lumière).

Mais l'effet est plus frappant encore que dans l'expérience EPR, et nous pose avec une force plus grande encore la question : qu'est-ce que le temps ?

Enjeux et interprétations - complément

Considérons la situation où la "gomme quantique" est présente. La complémentarité des figures d'interférence obtenues par corrélation des points reçus sur l'écran I avec les signaux reçus en G et H est une donnée importante qui doit être interprétée. On nommera ces figures Fig(G) et Fig(H). On appellera de même Fig(0) la figure obtenue en absence d'interférences.

Si la figure d'interférence était identique dans les deux cas (Fig(G) = Fig(H)), l'impact d'un photon sur une frange sombre de cette figure pourrait donner une information de type probabiliste. Nous pourrions dire dans ce cas qu'il y a davantage de chance de détecter le photon en J ou K (cas où il n'y a pas interférence car on détecte quel chemin le photon a emprunté) qu'en G ou H (cas où il y a interférence car la détection en G ou H n'apporte pas d'information sur le chemin emprunté).

Mais ce n'est pas le cas : les figures d'interférence sont exactement complémentaires (Fig(G)+Fig(H)=Fig(0)). Si le photon tombe sur une frange sombre de Fig(G) alors cela donne bien une information de type probabiliste : si le photon est détecté en G ou H alors le photon a davantage de chance d'être détecté en H (probabilité d'être détecté en H sachant qu'il est détecté en G ou en H). Mais cette information n'a aucun lien avec la connaissance du chemin emprunté par le photon.

Mathématiquement, la fonction d'onde juste après les convertisseurs bas s'écrit :

On a noté ψ la fonction d'onde d'un photon signal et φ celle d'un photon témoin. Juste avant l'impact sur l'écran I, on a :

La probabilité d'impact en un point x de l'écran est :

Les fonctions | ψ_B > et | ψ_C > sont orthogonales donc :

Il n'y a pas d'interférence. L'observation d'un impact en un point x₀ réduit la fonction d'onde du photon signal à | φ_I(x₀) > . Il s'agit d'une constante que l'on peut éliminer dans la suite. L'espace se réduit donc à un espace à une seule particule :

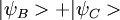
Dans l'expérience de Marlan Scully décrite un peu plus précisément dans l'article de Kim, la particule témoin prend la différence de phase de la particule signal. Comme après l'observation sur l'écran on connaît cette différence de phase, on a :

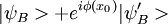
Comme les miroirs semi-réfléchissants introduisent des déphasages de Π / 2, on a finalement au niveau des détecteurs finaux :

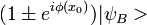
Le signe + ou - dépend du détecteur G ou H. On observe donc la corrélation avec la première observation car la différence de phase a été "enregistrée" dans la deuxième particule. Il n'y a donc aucune transmission d'une information du futur vers le passé : la connaissance du résultat x0 de la mesure en I pour le photon signal modifie, pour l'observateur, la probabilité de détection du photon témoin en G ou en H, de telle manière qu'apparaisse une figure d'interférence. La mécanique quantique explique correctement cette expérience de façon déterministe. Il n'y aurait pas eu de corrélation si expérimentalement la particule témoin n'avait pas pris la différence de phase de la particule signal.

Voir aussi

• Expérience d'Aspect
• Gomme quantique
• David Deutsch
• Freeman Dyson
• Hugh Everett
• John Wheeler
• Vitesse supraluminique
• Interféromètre de Mach-Zehnder
• Interprétation transactionnelle de la mécanique quantique

Notes

Liens externes

• Article sur l'expérience

L'expérience décrite dans cet article provient de l'article suivant :

• « A Delayed Choice Quantum Eraser » by Yoon-Ho Kim [1], R. Yu, S.P. Kulik, Y.H. Shih, and Marlon O. Scully Phys.Rev.Lett. 84 1-5 (2000) [1]
• Cette même expérience est décrite dans cette excellente présentation.

Voir aussi :

• (en) Détails
• (en) Expérience illustrée
• (en) Nouvelle expérience de « choix différé » allant dans le même sens, d'Alain Aspect.

• Portail de la physique