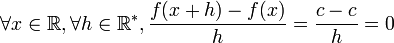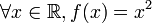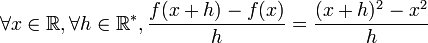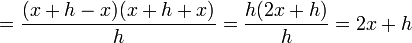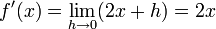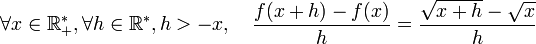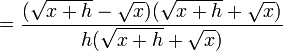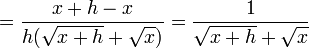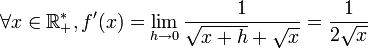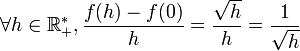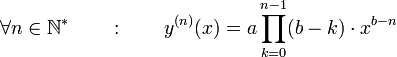- Exemples De Calcul De Dérivée
-
Exemples de calcul de dérivée
Voir dérivée pour plus d'informations globales.
La dérivée est une fonction mathématique, plus précisément une fonction de fonctions car elle prend comme argument d’entrée une fonction et renvoie une autre fonction, généralement différente.
Sommaire
Exemples à partir de la définition du nombre dérivé
Fonction constante
Soit c un réel.
Considérons la fonction constante f de valeur c :
donc
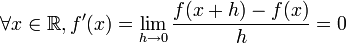 .
.
Ainsi la dérivée d’une fonction constante est la fonction nulle.
Fonction puissance énième
Démonstration :
Soit la fonction f:
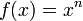 définie sur
définie sur 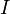
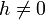
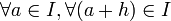
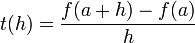
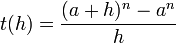
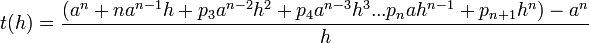
Où les coefficients pi sont donnés par le triangle de Pascal ( p1 = 1 et p2 = n). Les an s'annulent, on simplifie par h .
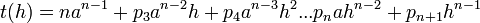
Donc :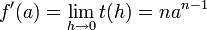
NB: fonctionne pour tout n et permet de retrouver les dérivées des fonctions inverse et racines énième. Cependant si n < 2 alors la fonction n'est pas dérivable en 0.Fonction carré
Considérons la fonction f définie sur
 par
pardonc
la dérivée de f est donc la fonction f’ définie par
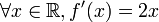 .
.
Fonction racine
Considérons la fonction f=√x
donc
D’autre part,
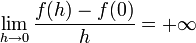
donc f n’est pas dérivable en 0 et la courbe représentative admet en 0 une demi tangente verticale.
Exemples à partir des formules de dérivées
Voici une série d'exemples de dérivées calculées à partir des formules établies par la méthode avec la limite.
Second degré
Considérons les fonctions suivantes et puis dérivons-les par la suite :
1.
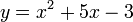
2.
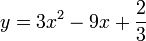
3.
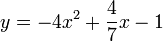
Dérivées : 1.
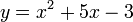
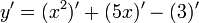
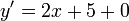
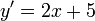
2.
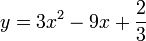
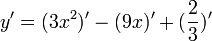
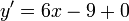
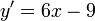
3.
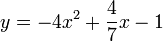
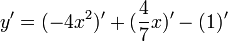
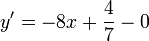
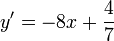
Troisième degré
Considérons les fonctions suivantes et dérivons-les par la suite :
1.
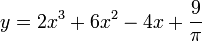
2.
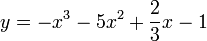
3.
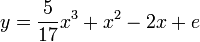
Dérivées :
1.
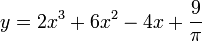
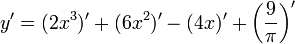
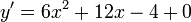
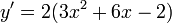
2.
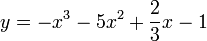
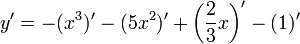
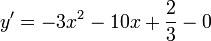
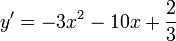
3.
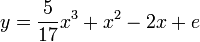
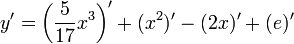
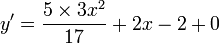
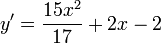
Fonction puissance réelle
Soit la fonction puissance y :
Alors, la dérivée n-ième de y est donnée, sur des intervalles convenables, par :
- Portail des mathématiques
Catégorie : Analyse réelle
Wikimedia Foundation. 2010.