Equation de Helmholtz
- Equation de Helmholtz
-
Équation de Helmholtz
L'équation de Helmholtz (d'après le physicien Hermann von Helmholtz) est une équation aux dérivées partielles elliptique qui apparaît lorsque l'on cherche des solutions stationnaires de l'équation de propagation des ondes de d'Alembert, appelées « modes propres », sur un domaine 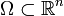 :
:
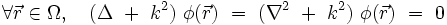
Pour que le problème mathématique soit bien posé, il faut spécifier une condition aux limites sur le bord 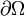 du domaine, typiquement :
du domaine, typiquement :
- soit la condition de Dirichlet (le champ scalaire est nul sur le bord),
- soit la condition de Neumann (la dérivée normale du champ scalaire est nulle sur le bord).
Lorsque le domaine Ω est compact, le spectre du Laplacien est discret, et les modes propres forment un ensemble dénombrable infini :

L'équation de Helmholtz se généralise en géométrie non-euclidienne en remplaçant le Laplacien par l'opérateur de Laplace-Beltrami sur une variété riemannienne.
Voir aussi
 Portail des mathématiques
Portail des mathématiques Portail de la physique
Portail de la physique Portail de la musique
Portail de la musique
Catégories : Équation aux dérivées partielles | Physique théorique | Acoustique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Equation de Helmholtz de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Équation de helmholtz — L équation de Helmholtz (d après le physicien Hermann von Helmholtz) est une équation aux dérivées partielles elliptique qui apparaît lorsque l on cherche des solutions stationnaires de l équation de propagation des ondes de d Alembert, appelées… … Wikipédia en Français
Équation de Helmholtz — L équation de Helmholtz (d après le physicien Hermann von Helmholtz) est une équation aux dérivées partielles elliptique qui apparaît lorsque l on cherche des solutions stationnaires de l équation de propagation des ondes de d Alembert, appelées… … Wikipédia en Français
Equation de Schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Equation de schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de Schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de Shroedinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de schrödinger — Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Helmholtz equation — The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation:( abla^2 + k^2) A = 0where abla^2 is the Laplacian, k is a constant, and the unknown function A=A(x, y, z) is defined on n dimensional… … Wikipedia
Équation de Schrödinger — L équation de Schrödinger, conçue par le physicien autrichien Erwin Schrödinger en 1925, est une équation fondamentale en physique quantique non relativiste. Elle décrit l évolution dans le temps d une particule massive non relativiste, et… … Wikipédia en Français
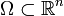 :
: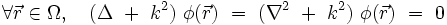
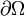 du domaine, typiquement :
du domaine, typiquement :
