- Affinité (Mathématiques)
-
Affinité (mathématiques)
 Pour les articles homonymes, voir Affinité.
Pour les articles homonymes, voir Affinité.En mathématiques, en géométrie en particulier, une affinité est une application affine ou linéaire égale à l'identité dans une direction et à une homothétie dans une autre.
Affinité vectorielle
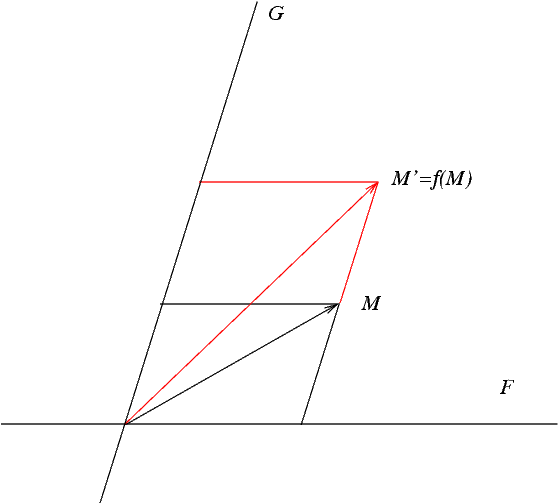 Figure 1. Construction d'une affinité
Figure 1. Construction d'une affinitéLes affinités vectorielles sont les endomorphismes qui sont somme directe de l'identité et d'une homothétie. Plus précisément :
Soit
 un espace vectoriel et deux sous espaces supplémentaires
un espace vectoriel et deux sous espaces supplémentaires  et
et  (
(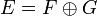 ) ;
) ;l'affinité de base
 (ou sur
(ou sur  ), de direction
), de direction  et de rapport
et de rapport 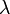 est l'unique endomorphisme
est l'unique endomorphisme  qui se restreint à
qui se restreint à  en l'identité, et à
en l'identité, et à  en l'homothétie de rapport
en l'homothétie de rapport 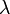 :
:Si
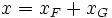 alors
alors 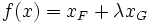 .
.Caractérisation en dimension finie : endomorphisme diagonalisable ayant deux valeurs propres au plus dont une est l'unité.
Les affinités recouvrent :
- l'identité (
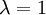 )
) - les projections, ou projecteurs (
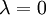 )
) - les symétries, ou involutions linéaires (
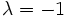 ), se réduisant à l'identité si la caractéristique du corps est 2)
), se réduisant à l'identité si la caractéristique du corps est 2) - les homothéties (
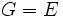 )
) - les dilatations, ou affinités hyperplanes, (
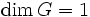 ).
).
Affinité ponctuelle
Étant donné un sous-espace affine
 d'un espace affine
d'un espace affine  associé à
associé à 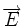 et une direction supplémentaire
et une direction supplémentaire 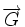 , l'affinité de base
, l'affinité de base  (ou sur
(ou sur  ) de direction
) de direction 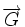 et de rapport λ est l'application définie par la construction :
et de rapport λ est l'application définie par la construction :- pour tout point
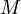 dans
dans  on trace l'unique sous-espace
on trace l'unique sous-espace 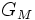 passant par
passant par 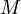 et de direction
et de direction 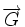 ;
; 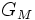 coupe
coupe  en un point unique
en un point unique 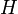 ;
;- l'image de
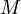 par
par  est alors le point
est alors le point 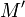 tel que
tel que 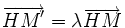 .
.
Les applications affines de partie linéaire une affinité vectorielle sont des affinités ponctuelles à condition d'avoir au moins un point fixe ; dans le cas général, on obtient des affinités glissées, composées d'une affinité et d'une translation de vecteur parallèle à la direction de l'affinité.
- Portail de la géométrie
Catégories : Géométrie affine | Transformation géométrique - l'identité (
Wikimedia Foundation. 2010.
