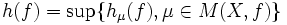Entropie (mathematiques)

Entropie (mathematiques)

Entropie (mathématiques)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Entropie (homonymie).

En mathématiques, l'entropie est une quantité réelle mesurant en un certain sens la complexité d'un système dynamique.

Entropie topologique

Article détaillé : entropie topologique.

Entropie métrique

Article détaillé : entropie métrique.

Théorème du principe variationnel

Article détaillé : Théorème du principe variationnel.

Le théorème du principe variationnel permet de faire le lien entre l'entropie topologique et l'entropie métrique. Pour tout homéomorphisme f d'un espace topologique séparé compact, il existe au moins une mesure borélienne invariante. Dans sa forme la plus simple, le théorème du principe variationnel affirme que l'entropie topologique de f est le supremum des entropies métriques de f associées aux différentes mesures boréliennes invariantes. Sous sa forme forte, le théorème affirme de plus que ce supremum est un maximum :

Théorème du principe variationnel

Forme faible : Pour tout système dynamique topologique compact (X,f), l'entropie topologique h(f) verifie :

h(f)=\sup \{ h_{\mu}(f), \mu\in M(X,f)\}

ou hμ(f) est l'entropie métrique de f associée à la mesure μ et M(X,f) est l'ensemble des mesures boréliennes de X qui soient f-invariantes.

Forme forte : Pour tout système dynamique topologique compact (X,f), il existe une mesure borélienne μ qui soit f-invariante, telle que l'entropie métrique de f pour μ soit exactement l'entropie topologique de f :

h(f) = hμ(f)

La forme faible se déduit de la forme forte et d'inégalités entre entropie topologique et entropie métrique.

La forme forte se démontre en chossissant la mesure / mu comme une limite faiblement convergente d'une suite de mesures.

Ce document provient de « Entropie (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Entropie (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Entropie (Mathématiques) — Pour les articles homonymes, voir Entropie (homonymie). En mathématiques, l entropie est une quantité réelle mesurant en un certain sens la complexité d un système dynamique. Entropie topologique Article détaillé : entropie topologique.… …   Wikipédia en Français

  • Entropie (mathématiques) — Pour les articles homonymes, voir Entropie (homonymie). En mathématiques, l entropie est une quantité réelle mesurant en un certain sens la complexité d un système dynamique. Entropie topologique Article détaillé : entropie topologique.… …   Wikipédia en Français

  • Entropie Topologique — En mathématiques et plus précisément, dans la théorie des systèmes dynamiques, l entropie topologique est un réel associé à tout homéomorphisme d un espace topologique séparé et compact. Ce réel caractérise l action induite de l homéomorphisme… …   Wikipédia en Français

  • Entropie De Shannon — L entropie de Shannon, due à Claude Shannon, est une fonction mathématique qui, intuitivement, correspond à la quantité d information contenue ou délivrée par une source d information. Cette source peut être un texte écrit dans une langue donnée …   Wikipédia en Français

  • Entropie de shannon — L entropie de Shannon, due à Claude Shannon, est une fonction mathématique qui, intuitivement, correspond à la quantité d information contenue ou délivrée par une source d information. Cette source peut être un texte écrit dans une langue donnée …   Wikipédia en Français

  • MATHÉMATIQUES , DE LA DIVERSITÉ À L’UNIFICATION — «Ce que nous appelons la réalité objective, c’est, en dernière analyse, ce qui est commun à plusieurs êtres pensants, et pourrait être commun à tous; cette partie commune [...], ce ne peut être que l’harmonie exprimée par des lois mathématiques.» …   Encyclopédie Universelle

  • Entropie Métrique — L entropie métrique, ou entropie de Kolmogorov (se dit aussi en anglais measure theoretic entropy) est un outil développé par Kolmogorov vers le milieu des années 1950 issu du concept probabiliste d entropie de la théorie de l information de… …   Wikipédia en Français

  • Entropie metrique — Entropie métrique L entropie métrique, ou entropie de Kolmogorov (se dit aussi en anglais measure theoretic entropy) est un outil développé par Kolmogorov vers le milieu des années 1950 issu du concept probabiliste d entropie de la théorie de l… …   Wikipédia en Français

  • Entropie (thermodynamique) — Entropie Pour les articles homonymes, voir Entropie (homonymie). En thermodynamique, l entropie est une fonction d état introduite en 1865[1] par Rudolf Clausius dans le cadre du deuxième principe, d après les travaux de Sadi Carnot[ …   Wikipédia en Français

  • Entropie (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”