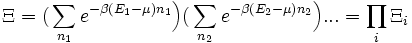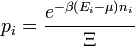- Ensemble macrocanonique
-
Ensemble grand-canonique
En physique statistique, l’ensemble grand-canonique est un ensemble statistique, dans lequel chaque système est en équilibre avec un réservoir externe d'énergie et de particules. Cela signifie que le système peut échanger de l’énergie et des particules avec le réservoir, autrement dit, l’énergie et le nombre de particules sont alors amenés à fluctuer d’un système à un autre de l’ensemble.
Cet ensemble est utilisé lorsque le nombre de particules ne peut pas être fixé, plus particulièrement pour les systèmes composés de bosons et de fermions.
Sommaire
Introduction
Dans cet ensemble, on considère que le système est composé de particules identiques[1], et on introduit le potentiel chimique, pour prendre en considération la variation du nombre de particules. Le réservoir doit être considéré grand devant le système, afin que les échange d’énergie et de particules n’influent pas[2] sur la température du réservoir, et donc sur la température du système. Le réservoir doit alors se comporter comme un thermostat et imposer sa température au système.
On considère l’hamiltonien[3] du système défini comme :
où
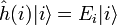 est l’équation de Schrödinger pour chaque particule i.
est l’équation de Schrödinger pour chaque particule i.Pour chaque ensemble miscrocopique
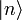 , on a alors l’énergie et le nombre de particules associés :
, on a alors l’énergie et le nombre de particules associés :Suivant que le système considéré est composé de bosons, ou de fermions, ni est soumis aux conditions suivantes :
Observable miscrocopique
Fonction de partition
La fonction de partition est définie comme étant :
où
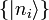 représente l’ensemble statistique de tous les ensemble miscrocopique
représente l’ensemble statistique de tous les ensemble miscrocopique 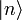 .
.On peut[3] écrire Ξ comme :
avec
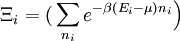 , qui représente la fonction de partition d'un système d'une seule particule.
, qui représente la fonction de partition d'un système d'une seule particule.Probabilité d'un micro-état
La probabilité pour que le système soit dans un micro-état i est défini par :
où
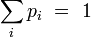
Observables macroscopique
Notes
Voir aussi
Articles connexes
Tableau résumant
les ensembles
en physique statistiqueEnsembles Microcanonique Canonique Grand-canonique Variables indépendantes E, N, V ou B T, N, V ou B T, μ, V ou B Fonction microscopique nombre des micro-états
ΩFonction de partition canonique
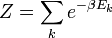
Fonction de partition grand-canonique
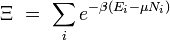
Potentiel thermodynamique Entropie
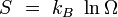
Energie libre
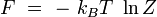
Grand potentiel
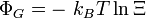
Bibliographie
- Claudine Guthmann, Danielle Lederer et Bernard Roudet, Éléments de physique statistique, 1996 [détail des éditions]
- Frederic Reif, Physique Statistique, Cours de Physique de Berkeley (vol. 5), Armand Colin (1972) 398 pp. réédité par Dunod.
- Portail de la physique
Catégorie : Physique statistique
Wikimedia Foundation. 2010.

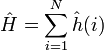
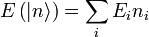
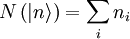
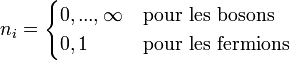
![\Xi = \sum_{\{|n_i\rangle\} } e^{ -\beta \big[ E \left(|n\rangle\right) - \mu N\left(|n\rangle\right)\big] } = \sum_{ \{ |n_i \rangle \} } e^{ -\beta \sum_i \left(E_i - \mu \right)n_i }](/pictures/frwiki/48/01bde60818ad303fc1e197dbd21b7f29.png)