- Ensemble Transitif
-
Ensemble transitif
En mathématique, un ensemble transitif est un ensemble E composé d'éléments, qui sont aussi des ensembles, et dont les éléments appartiennent aussi à l'ensemble initial E.
Sommaire
Définition
En théorie des ensembles, un ensemble X est dit transitif
- si et seulement si tout élément y d’un élément x de X est lui-même élément de X
ou encore
- si et seulement si tout élément x de X est un sous-ensemble de X ; en langage symbolique :
- ∀ x (x ∈ X ⇒ x ⊂ X)
On parle également de classe transitive, avec la même définition : tout ensemble élément de la classe est également sous-ensemble de celle-ci.
Exemples
- Les ordinaux de John von Neumann sont en particulier des ensembles transitifs[1] :
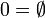 ,
, 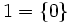 ,
, 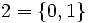 ,
, 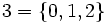 ,
, 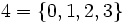 ,
, 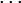 ,
, 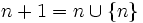 , etc.
, etc.- Par exemple, pour l’ordinal
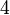 on a
on a 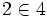 et
et 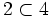 .
.
En effet
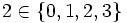 et
et 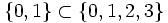 .
.- La classe de tous les ordinaux est une classe transitive : les éléments d'un ordinal sont des ordinaux.
- Le couple (0,1), défini par { {∅}, {∅,{∅}} }, est un ensemble qui n'est pas transitif : {∅} ∈ (0,1) et ∅ ∉ (0,1).
- En théorie des ensembles (Z, ZF, ZFC...), pour tout ensemble X, il existe un unique ensemble transitif Y contenant X et contenu dans tout ensemble transitif contenant X. On l'appelle clôture transitive de X. La clôture transitive est définie par induction sur les entiers naturels, en prenant la réunion des éléments de X, puis la réunion des ensembles obtenus etc. (on note ∪A la réunion des éléments de A) :
-
- Y0=X ; Yn+1=∪Yn ; Y = ∪n ∈ NYn
- On montre que Y est bien transitif : si x ∈ Y, alors pour un certain entier n, x ∈ Yn, et donc, par construction de Yn+1, x ⊂ Yn+1.
- On montre par récurrence sur l'entier n que tout ensemble transitif contenant X contient Yn.
- On appelle P(A) l'ensemble des parties de A, c'est-à-dire tous les sous-ensembles de A. On définit par induction sur les entiers naturels (N désigne l'ensemble des entiers naturels) :
-
- V0=∅ ; Vn+1=P(Vn)
- et on pose Vω=∪n ∈ N Vn.
- Les Vn pour n entier naturel, et Vω sont des ensembles transitifs. On peut généraliser cette construction par induction sur la classe de tous les ordinaux pour obtenir une classe transitive V. Dans un modèle de ZFC, on montre (voir la référence indiquée) que Vω définit un ensemble qui, muni de la même relation d'appartenance, est modèle de tous les axiomes de ZFC sauf l'axiome de l'infini. Celui-ci est donc indépendant des autres axiomes. De façon analogue, la classe V définit, dans un modèle de ZFC sans axiome de fondation, un modèle de ZFC avec axiome de fondation. Sans entrer dans le détail de ces preuves (et de la définition de V), on comprend bien que pour construire un modèle de la théorie des ensembles comme une sous-classe d'un autre modèle, en conservant la même relation d'appartenance, il faut que cette sous-classe soit transitive.
Notes
- ↑ Les ordinaux de Von Neumann sont définis comme ensembles transitifs bien ordonnés par l'appartenance, en tant qu'ordre strict.
Voir aussi
Références
- Jean-Louis Krivine, « Théorie des Ensembles », Paris, éditions Cassini, collection Nouvelle Bibliothèque Mathématique, 1998 (ISBN 2-84225-014-1)
- Portail des mathématiques
Catégorie : Théorie des ensembles
Wikimedia Foundation. 2010.
