Décomposition-arbre

En théorie des graphes, la décomposition arborescente (en anglais : tree-decomposition) consiste en la décomposition d'un graphe en séparateurs connectés dans un arbre. Cette méthode a été proposée par Seymour et Robertson dans le cadre de leur théorie sur les mineurs d'un graphe.

Définition

Étant donné un graphe G = (V,E), une décomposition arborescente de G est un couple (X,T), où 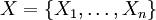est une famille de sous-ensembles de sommets de V, et T est un arbre dont les nœuds sont étiquetés par ces sous-ensembles X_i, tels que :

• l'union de tous les X_i de X est égale à V ;
• pour toute arête (v,w) de E, il existe un nœud X_i de l'arbre T qui contient v et w ;
• si X_i et X_j contiennent un même sommet v, alors tous les nœuds X_z de T sur le chemin entre X_i et X_j contiennent v.

Cette dernière condition est équivalente au fait que tous les nœuds X_i de l'arbre T contenant un nœud v de G induisent un sous-arbre de T.

Utilisations

Cette méthode s'applique lorsque l'on cherche à résoudre un problème combinatoire dont le graphe fait partie de la donnée. L'idée est de résoudre le problème initial sur chacun des sous-ensembles de la décomposition, puis de fusionner les résultats dans l'arbre à l'aide de méthodes de programmation dynamique. La méthode ne s'applique que pour des problèmes bien particuliers, la coloration de graphes, par exemple.

Largeur arborescente

Cette décomposition n'est pas unique. Le minimum (pris parmi toutes ces décompositions) de la taille moins un du plus grand sous-ensemble est appelée largeur arborescente (treewidth) du graphe. Cette valeur détermine donc l'intérêt d'utiliser la méthode de décomposition. Le calcul de la largeur arborescente est NP-difficile. Néanmoins, si k est fixé, il existe un algorithme linéaire pour déterminer si la largeur arborescente d'un graphe est k. La dépendance en k du temps d'éxecution de l'algorithme dans le pire des cas est cependant exponentielle. Pour certaines classes particulières de graphes, calculer la largeur arborescente se fait en temps polynomial (arbres, graphes triangulés,… ).

Lorsque l'arbre n'est constitué que d'un chemin, on parle de décomposition linéaire (path-decomposition) et de largeur (arborescente) linéaire (pathwidth).

De nombreux problèmes de graphes NP-difficiles dans le cas général peuvent être résolus en temps polynomial si on se restreint aux graphes de largeur arborescente bornée. Si le problème est exprimable en logique monadique du second d'ordre, il peut même être résolu en temps linéaire, mais la constante est une tour d'exponentielles en k qui rend l'algorithme inapplicable en général.

Le concept de décomposition arborescente a un lien très fort avec les graphes triangulés. Premièrement, la largeur arborescente d'un graphe triangulé H est égale à la taille χ(H) de sa plus grande clique moins un. Deuxièmement, la valeur χ(H) peut être calculée à l'aide d'un algorithme linéaire si le graphe H est triangulé. Dans la littérature de recherche opérationnelle, les algorithmes de calcul de la largeur arborescente d'un graphe G cherchent souvent à déterminer le graphe triangulé H de plus petite valeur χ(H) qui contient G.

• Portail des mathématiques