Dominance strategique

En théorie des jeux, la dominance stratégique apparaît lorsqu'une stratégie est meilleure pour un joueur qu'une autre stratégie, quel que soit la stratégie de l'adversaire.

Définitions

Soit deux stratégies A et B envisageables par un joueur dans un jeu à information parfaite donné. B domine' A si le paiement associé à B est supérieur ou égal à celui associé à A pour toute stratégie de l'adversaire. S'il existe en outre une stratégie de l'adversaire telle que le paiement associé à B soit strictement supérieur à celui associé à A pour cette stratégie, alors B domine strictement A.

Ces définitions se généralisent naturellement à tout ensemble de stratégies :

• B est strictement dominante si elle domine strictement toutes les autres stratégies possibles.
• B est faiblement dominante si elle domine toutes les autres stratégies mais qu'il en existe au moins une qui ne soit pas strictement dominée par B.

Formulation mathématique

Soit un joueur i, S_i l'ensemble de ses stratégies et S _{− i} l'ensemble des stratégies de ses adversaires. Une stratégie 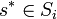domine faiblement une autre stratégie 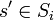si

avec au moins une inégalité stricte.

De même, s ^* domine strictement 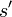si

Dominance stratégique et équilibre de Nash

S'il existe une stratégie dominante pour un joueur dans un jeu, alors cette stratégie sera jouée par ce joueur à l'équilibre de Nash du jeu. Si les deux joueurs ont une stratégie dominante, alors l'équilibre de nash est unique et se trouve à la rencontre de ces deux stratégies. Cet équilibre peut cependant ne pas être Pareto-optimal, comme dans le cas du dilemme du prisonnier.

Réciproquement, une stratégie strictement dominée ne peut être jouée à l'équilibre de Nash du jeu, mais une stratégie faiblement dominée peut l'être, comme dans le cas du jeu ci-contre : C domine faiblement D, mais (D,D) est un équilibre de Nash.

Élimination répétée des stratégies dominées

Une technique de résolution des jeux est l'élimination répétée des stratégies dominées. À la première étape, toutes les stratégies dominées sont éliminées du jeu, puisque les joueur ne vont pas les choisir à l'équilibre. Cela conduit à un nouveau jeu, plus réduit. Des stratégies qui n'étaient pas auparavant dominées peuvent le devenir, du fait de l'élimination de situations non pertinentes. On les élimine à leur tour, jusqu'à ce qu'il n'existe plus de stratégie dominée dans le jeu.

Si on a éliminé ainsi uniquement les stratégies strictement dominées et qu'il ne reste plus qu'une stratégie pour chaque joueur, on a déterminé l'équilibre de Nash du jeu.

Si on a éliminé aussi les stratégies faiblement dominées à chaque étape et qu'il ne reste qu'une stratégie par joueur, on obtient également un équilibre de Nash. Toutefois, il peut alors exister dans le jeu d'autres équilibres de Nash, et l'équilibre obtenu à la fin du procédé peut être différent selon l'ordre d'élimination des stratégies retenu.