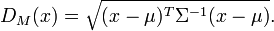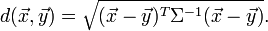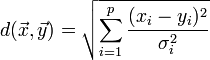Distance de mahalanobis

Distance de Mahalanobis

En statistique, la distance de Mahalanobis est une mesure de distance introduite par P. C. Mahalanobis en 1936^[1]. Elle est basée sur la corrélation entre des variables par lesquelles différents modèles peuvent être identifiés et analysés. C'est une manière utile de déterminer la similarité entre une série de données connues et inconnues. Elle diffère de la distance euclidienne par le fait qu'elle prend en compte la corrélation de la série de données. Ainsi, à la différence de la distance euclidienne où toutes les composantes des vecteurs sont traitées de la même façon, la distance de Mahalanobis accorde un poids moins important aux composantes les plus bruitées (en supposant que chaque composante soit une variable aléatoire de type gaussien).

La distance de Mahalanobis est souvent utilisée pour la détection de données aberrantes dans un jeu de données, ou bien pour déterminer la cohérence de données fournies par un capteur par exemple : cette distance est calculée entre les données reçues et celles prédites par un modèle.

En pratique, la distance de Mahalanobis d'une série de valeurs de moyenne 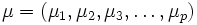$\mu = ( \mu_1, \mu_2, \mu_3, \dots , \mu_p )$ et possédant une matrice de covariance $Σ$ pour un vecteur à plusieurs variables 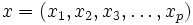$x = ( x_1, x_2, x_3, \dots, x_p )$ est définie comme suit:

$D_M(x) = \sqrt{(x - \mu)^T \Sigma^{-1} (x-\mu)}.\,$

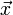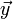La distance de Mahalanobis peut aussi être définie comme étant la mesure de dissimilarité entre deux vecteurs aléatoires $\vec{x}$ et $\vec{y}$ de même distribution avec une matrice de covariance $Σ$ :

$d(\vec{x},\vec{y})=\sqrt{(\vec{x}-\vec{y})^T\Sigma^{-1} (\vec{x}-\vec{y})}.\,$

Si la matrice de covariance est la matrice identitaire, cette distance est alors la même que la distance euclidienne. Si la matrice de covariance est diagonale, elle est appelée distance euclidienne normalisée:

$d(\vec{x},\vec{y})= \sqrt{\sum_{i=1}^p {(x_i - y_i)^2 \over \sigma_i^2}}$

où $σ i$ est l'écart type de $x i$ sur la série de données.

Cette distance est souvent utilisée en analyse des données. (ex: analyse discriminante)

Références

↑ (en) P C Mahalanobis, « On the generalised distance in statistics », dans Proceedings of the National Institute of Sciences of India, vol. 2, n^o 1, 1936, p. 49–55 [texte intégral]

Portail des probabilités et des statistiques

Ce document provient de « Distance de Mahalanobis ».

Catégorie : Statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Distance de mahalanobis de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Distance De Mahalanobis — En statistique, la distance de Mahalanobis est une mesure de distance introduite par P. C. Mahalanobis en 1936[1]. Elle est basée sur la corrélation entre des variables par lesquelles différents modèles peuvent être identifiés et analysés. C est… … Wikipédia en Français
Distance de Mahalanobis — En statistique, la distance de Mahalanobis est une mesure de distance introduite par P. C. Mahalanobis en 1936[1]. Elle est basée sur la corrélation entre des variables par lesquelles différents modèles peuvent être identifiés et analysés. C est… … Wikipédia en Français
Distance de Bhattacharyya — En statistiques, la distance de Bhattacharyya est une mesure de la similarité de deux distributions de probabilités discrètes. Elle est reliée au coefficient de Bhattacharyya , qui est une mesure statistique du recouvrement de deux ensembles d… … Wikipédia en Français
Mahalanobis distance — In statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936.[1] It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown… … Wikipedia
Mahalanobis-Abstand — Die Mahalanobis Distanz (nach Prasanta Chandra Mahalanobis) ist ein Distanzmaß zwischen Punkten in einem mehrdimensionalen Vektorraum. Die Mahalanobis Distanz wird speziell in der Statistik zum Beispiel im Zusammenhang mit multivariaten Verfahren … Deutsch Wikipedia
Mahalanobis Abstand — Die Mahalanobis Distanz (nach Prasanta Chandra Mahalanobis) ist ein Distanzmaß zwischen Punkten in einem mehrdimensionalen Vektorraum. Die Mahalanobis Distanz wird speziell in der Statistik zum Beispiel im Zusammenhang mit multivariaten Verfahren … Deutsch Wikipedia
Mahalanobis-Distanz — Die Mahalanobis Distanz (nach Prasanta Chandra Mahalanobis) ist ein Distanzmaß zwischen Punkten in einem mehrdimensionalen Vektorraum. Die Mahalanobis Distanz wird speziell in der Statistik zum Beispiel im Zusammenhang mit multivariaten Verfahren … Deutsch Wikipedia
Distance — This article is about distance in the mathematical or physical sense. For other senses of the term, see distance (disambiguation). Proximity redirects here. For the 2001 film, see Proximity (film). Distance (or farness) is a numerical description … Wikipedia
Prasanta Chandra Mahalanobis — P.C. Mahalanobis Born 29 June 1893( … Wikipedia
Distancia de Mahalanobis — Saltar a navegación, búsqueda En estadística, la Distancia de Mahalanobis es una medida de distancia introducida por Mahalanobis en 1936. Su utilidad radica en que es una forma de determinar la similitud entre dos variables aleatorias… … Wikipedia Español

Dictionnaires et Encyclopédies sur 'Academic'

Distance de mahalanobis