Distance Orthoscopique

Note :

Il est vivement conseillé de consulter également les articles suivants :

• Diaphragme
• Performances de l'œil
• Iris et diaphragme
• Distance orthoscopique
• Flou, netteté et contraste
• Profondeur de foyer
• Profondeur de champ

qui forment un ensemble cohérent et sont nécessaires à la compréhension de ce dernier article.

Note : Cet article est initialement issu de celui intitulé profondeur de champ qui a fait l'objet d'un découpage pour former ou compléter les articles mentionnés ci-dessus.

---

Pour qu'une photographie soit aussi réaliste que possible, il faut théoriquement la regarder sous un angle identique à celui sous lequel l'appareil « voyait » le sujet. La distance d'observation qui permet de restituer cet angle de vision s'appelle distance orthoscopique. Elle n'est pas souvent respectée, même approximativement, pourtant c'est elle qui doit être prise pour base de tout calcul sérieux de la profondeur de champ ...

Mais d'abord, quelques rappels élémentaires de perspective :

A	B	C

Les photos A et B ont été prises du même endroit en faisant varier la distance focale du zoom dans un rapport d'environ 3,5. En agrandissant la zone centrale de la photo A dans le même rapport, on obtiendrait une image notablement dégradée mais exactement superposable à la photo B. La photo C a été prise d'un point plus rapproché que les photos A et B et agrandie de façon que la hauteur de la maison (signée Le Corbusier) soit conservée. La perspective a changé, on voit sur la photo C des détails du bâtiment qui n'apparaissaient pas sur A et B. Dans le même temps, les proportions des objets sont profondément modifiées. S'il fallait vendre quelque chose, ce serait sans aucun doute la maison sur la photo B et la voiture sur la photo C.

La perspective ne dépend que du point de vue.

Sur votre écran, les trois images sont situées dans le même plan et il est hautement probable que vous n'en observiez actuellement aucune à la bonne distance ! Vous êtes vraisemblablement un peu trop loin de la photo B, qui a été prise en position téléobjectif, et beaucoup trop loin des photos A et C, qui ont été prises en position grand-angulaire.

Il est clair que pour apprécier convenablement la netteté d'une image, il faut la regarder à la bonne distance. Trop loin, les défauts disparaissent, trop près, on en trouve qui n'en sont pas.

Profitons-en pour tordre le cou à une autre idée reçue. Sauf s'ils sont affectés d'une distorsion monstrueuse qui traduit les lignes droites du sujet par des lignes courbes sur l'image, les téléobjectifs et les grand-angulaires ne déforment pas les images. Les déformations apparentes qui leur sont injustement imputées se produisent uniquement lorsque les images ne sont pas examinées depuis la bonne distance.

Appelons D la distance orthoscopique. Comment la calcule-t-on ?

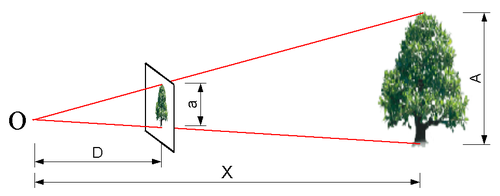
Prenons un élément du sujet, par exemple un arbre de hauteur A situé, au moment de la prise de vue, à une distance X de l'objectif O.

Sur la photographie, l'image de cet arbre aura une hauteur a ; le rapport G=a/A est appelé grandissement. Pour respecter l'angle de vision, il faut alors que : 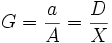, autrement dit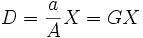

Prenons le cas de la photo B : l'immeuble a une hauteur d'environ 10 m (trois niveaux plus une terrasse) et la photo a été prise depuis une distance de l'ordre de 50 m. Sur un écran de 19 pouces paramétré en 1024x768 pixels, l'image de l'immeuble mesure 7 cm, donc, en convertissant toutes les distances en cm :

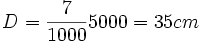
Compte tenu de la variation de focale effectuée entre A et B (3,5), il s'ensuit que la photo A devrait être vue depuis une distance d'environ 10 cm. Pour la photo C, ce serait plutôt à 6 à 7 cm. Naturellement, si votre écran est plus petit, ces distances doivent être diminuées en proportion. Finalement, seule la photo B correspondra à une vision pas trop déformée ...

Remarques :

• le grandissement G est en réalité le produit de deux grandissements successifs, g

qui correspond au rapport entre les dimensions de l'image formée sur le film ou le capteur et celles du sujet, puis g' qui correspond au passage de l'image enregistrée sur film ou dans la carte-mémoire à celle qui est finalement observée sur un tirage papier ou un écran de projection. G = g.g'

• la plupart du temps, l'image finale est beaucoup plus petite que le sujet, le grandissement est en réalité une réduction, on trouve G<1, avec g<<1 et g'>1.
• dans le cas de la macrophoto proprement dite, l'image enregistrée par l'appareil est plus

grande que le sujet, on trouve alors G>1, avec g>1 et g'>1.

• il peut arriver que l'image finale soit plus grande que le sujet ; c'est toujours le cas en

macrophotographie, mais pas seulement : les Grands nus d'Helmut Newton sont des tirages photographiques plus grands que les modèles.

Voir aussi

• wikilivre de photographie - chapitre 14 : Netteté des images photographiques

• Portail de la photographie
• Portail de la physique