Diagramme (jonglerie)

Les diagrammes sont des graphes utilisés en jonglerie pour décrire et inventer des figures. Les diagrammes sont associés aux différentes notations algébriques utilisées, la plus commune étant le siteswap. Certains servent à représenter plus intuitivement des séquences siteswaps, d’autres permettent de vérifier leur validité, de déterminer les transitions entre les différentes séquences, et enfin de répertorier l’ensemble des séquences possibles pour un nombre d’objets donné. Ils sont ainsi un outil indispensable pour tirer parti des diverses notations jonglistiques et en comprendre la logique.

Sommaire 1 Diagramme en échelle 2 Diagramme de cause 3 Diagramme états-transitions 3.1 Graphe complet classique 3.2 Graphe réduit 4 Liens externes

Diagramme en échelle

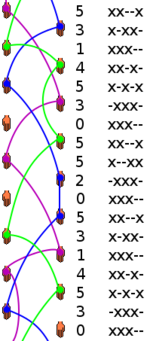
Les diagrammes en échelle, également appelés diagrammes d’espace temps par analogie avec ceux utilisés en physique, sont la forme la plus simple pour représenter schématiquement une séquence de jonglerie. Inventé en 1982 par Jeff Walker (Variations for Numbers Jugglers dans Juggler’s World, janvier 1982, p. 11), il s’agit d’un diagramme à deux dimensions (les sites de lancer - les deux mains ; et le temps) qui représente schématiquement le trajectoire des objets lancés lors de la séquence. Il correspond à l’image obtenue si l’on filmait en plongée un jongleur lançant les objets en avançant.

Les diagrammes en échelle permettent de représenter la plupart des séquences, qu’elles soient asynchrones (comme dans le cas présent) ou synchrones, qu’elles demandent un ou plusieurs jongleurs (dans ce dernier cas, il suffira de juxtaposer plusieurs « échelles » en parallèle).

Ces diagrammes s’utilisent principalement pour illustrer une séquence notée en siteswap ou inversement pour convertir une séquence jonglée en séquence siteswap. En effet, on peut (comme sur l’exemple de droite) associer la valeur siteswap du lancer à chaque « marche » de l’échelle, celle-ci correspondant simplement au nombre de marches jusqu’à la prochaine relance de l’objet. On peut également associer à chaque étape l’état correspondant (noté selon le passage du temps de gauche à droite, un x représentant un objet à relancer et - un temps vide). Ainsi, le diagramme de droite représente la séquence 53145305520 d’un siteswap vanille.

Diagramme de cause

Inventé par Martin Frost, le diagramme de cause est utilisé en passing pour représenter et inventer des séquences incluant plusieurs jongleurs. Le diagramme qui suit représente une séquence de passing classique à 6 objets pour deux jongleurs dite « 4-temps » ou « passe-passe » (notation siteswap <3p333|3p333>) :

Les deux séries horizontales RLRLRL… représentent les lancers de deux jongleurs alternant entre les lancers de la main droite (R pour l’anglais « right ») et la main gauche (L pour l’anglais « left »).

Diagramme états-transitions

Alors que les diagrammes en échelle et les diagrammes de cause ne représentent qu’une seule séquence à chaque fois, les diagrammes d’états ou diagrammes états-transitions représentent l’ensemble des séquences possibles pour un nombre d’objets et une longueur maximale de lancer donnés. Ils servent ainsi à recenser l’intégralité des séquences, inventer des séquences et des transitions entre ces diverses séquences.

Graphe complet classique

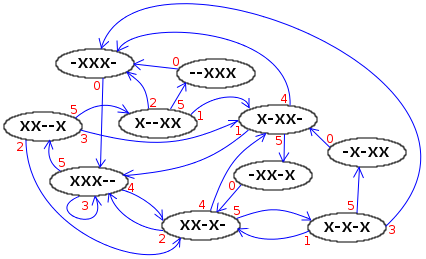
Un graphe transitions-états classique représente l’ensemble des états et des transitions possibles entre ces états. Le graphe de droite montre par exemple tous les états possibles pour 3 objets et un lancer maximal de 5. Ce graphe permet de recenser toutes les séquences existantes dans ces conditions c’est-à-dire 26 séquences siteswap premières et toutes les séquences composées qui en découlent. Pour construire une séquence valide, il suffit de partir d’un état, de suivre les flèches à sa guise en concaténant les valeurs des transitions rencontrées ; une fois revenu à l’état de départ la séquence siteswap obtenue sera valide. Lorsque l’état initial est l’état fondamental (plus petit état où tous les bits au plus bas), alors la séquence est dite première ; c’est une séquence indécomposable. Toutes les séquences peuvent être répertoriées par ce biais cependant ce type de graphe devient vite extrêmement complexe et illisible à mesure qu’augmente la hauteur des lancers. Le nombre d’états nécessaires pour une longueur maximale de n et un nombre d’objets k est le coefficient binomial .

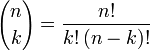Graphe réduit

Introduit en 2004 par Hans Lundmark, le graphe réduit propose une solution à la complexité des graphes complets. Bien que tous les états y soient virtuellement représentés on remplace les états qui n’ont qu’une seule transition d’entrée et une seule transition de sortie par une transition à deux chiffres, trois chiffres pour des chaînes d’états plus longues etc. L’application récursive de cette méthode permet de réduire considérablement le nombre d’états à représenter. L’exemple ci-contre comporte les mêmes informations que le graphe complet précédent avec seulement 3 états représentés au lieu de 10. Les transitions entre deux états se lisent avec les chiffres les plus proches de l’état de départ, ainsi pour passer de l’état fondamental 111 à l’état excité 1011 on met en œuvre soit la séquence 4 soit la séquence 52. Avec ce système, 10 états suffiront pour 4 objets et un lancer maximal de 7 contre 35 nécessaires dans le cas d’un graphe complet classique. Plus généralement, il suffira de représenter 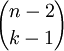états au lieu de 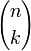pour k objets et un lancer maximal de n.

Liens externes

• Diagrammes de cause et SiteSwaps - Article de JiBe sur PassingDataBase décrivant les diagrammes de cause et leur utilisation en passing
• Diagrammes d’états et Siteswap - Article de Hans Lundmark introduisant les diagrammes d’état réduits (pdf)

• Portail de la jonglerie