- Deuxième quantification
-
Seconde quantification
La seconde quantification, aussi appelée quantification canonique, est une méthode de quantification des champs introduite par Dirac en 1927 pour l'électrodynamique quantique. Elle consiste à partir d'un champ classique tel que le champ électromagnétique, à le considérer comme un système physique et à remplacer les grandeurs classiques (E, B) décrivant l'état du champ par un état quantique et des observables de la physique quantique. On aboutit naturellement à la conclusion que l'énergie du champ est quantifiée, chaque quantum représentant une particule.
La seconde quantification a été baptisée ainsi par Fock et Jordan en 1932. En 1949, Pauli dira à Klein : «La seconde quantification, c'est le péché au carré.»
Sommaire
Exemple du champ scalaire réel
Pour simplifier les notations, on s'intéresse dans un premier temps à un champ scalaire réel. On pourrait par exemple penser au champ de pression P(r,t) dans un gaz, mais ce champ n'est pas fondamental, puisqu'il suppose l'existence d'autres particules et ne peut exister dans le vide. Le seul champ étudié en physique classique qui puisse se propager dans le vide est le champ électromagnétique, lequel est un champ tensoriel. On peut cependant construire un champ scalaire se propageant dans le vide en considérant la fonction d'onde d'une particule relativiste comme un champ.
Première quantification
L'équation relativiste donnant l'énergie E de la particule de masse m et de charge électrique nulle en fonction de sa quantité de mouvement
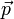 s'écrit :
s'écrit :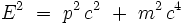
En appliquant une première fois les règles de la quantification canonique issues de la mécanique quantique, on obtient l'équation de Klein-Gordon pour la fonction d'onde
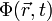 :
: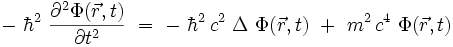
Cette équation se réécrit sous la forme suivante :
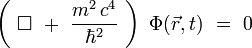
où
 représente l'opérateur d'Alembertien :
représente l'opérateur d'Alembertien :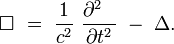
Si l'on a considéré jusqu'à présent que Φ était la fonction d'onde de la particule, on peut également la considérer comme un champ scalaire réel se propageant dans le vide, l'équation de Klein-Gordon étant son équation de propagation.
Développement de Fourier
Supposons pour simplifier que la particule soit confinée dans une grande boîte de volume V fini. Le champ scalaire
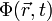 admet alors un développement en série de Fourier[1]. Notons :
admet alors un développement en série de Fourier[1]. Notons :- ω la variable conjuguée au temps t : ω est la pulsation.
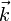 le vecteur conjugué à la position
le vecteur conjugué à la position 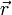 :
: 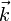 est le vecteur d'onde.
est le vecteur d'onde.
Les modes propres sont les exponentielles :
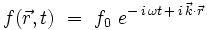
qui vérifient l'équation de Klein-Gordon :
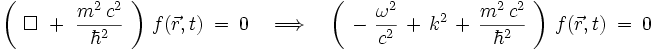
On doit donc avoir la relation de dispersion :
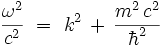
Donc, si l'on se donne un vecteur d'onde
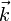 , il lui correspond deux modes propres de pulsations respectives :
, il lui correspond deux modes propres de pulsations respectives :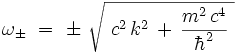
Le développement en série de Fourier du champ scalaire
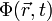 peut donc s'écrire comme une somme sur tous les vecteurs d'ondes possibles[2] :
peut donc s'écrire comme une somme sur tous les vecteurs d'ondes possibles[2] :![\Phi \left( \overrightarrow{r},t\right) =\sum_{\overrightarrow{k}}\left[
A_{+}e^{-i\omega _{+}t}+A_{-}e^{-i\omega _{-}t}\right] e^{i\overrightarrow{k}
.\overrightarrow{r}}+c.c.](/pictures/frwiki/101/e6e9d1f9480efacd7b5ad541dd05c61d.png)
où cc désigne le complexe conjugué.
Seconde quantification
La procédure de seconde quantification consiste à remplacer les coefficients complexes des modes de Fourier du développement du champ scalaire par des opérateurs abstraits :
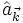 , appelé opérateur d'annihilation d'un quantum d'impulsion
, appelé opérateur d'annihilation d'un quantum d'impulsion 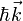 .
.
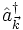 , appelé opérateur de création d'un quantum d'impulsion
, appelé opérateur de création d'un quantum d'impulsion 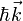 .
.
Ces opérateurs obéissent par définition à la règle de commutation canonique :![\left[ \ \hat{a}_{\vec{k'}}, \ \hat{a}_{\vec{k}}^{\dagger} \ \right] \ = \ \delta_{\vec{k}, \vec{k}'} \ \hat{1}](/pictures/frwiki/48/0e885561f90a340b43a5842002cbba50.png)
Le champ scalaire de spin zéro est donc un champ bosonique.
Notes et références
- ↑ Si le volume V de la boîte est infini, il faut utiliser la transformée de Fourier à la place de la série de Fourier.
- ↑ Il faut imposer une condition aux limites sur la frontière
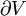 du volume fini V. C'est cette condition aux limites qui va provoquer la discrétisation des vecteurs d'ondes possibles. Si on prend par exemple des conditions aux limites périodiques pour un volume parallélépipédique : V = LxLyLz, cette quantification s'écrira explicitement :
du volume fini V. C'est cette condition aux limites qui va provoquer la discrétisation des vecteurs d'ondes possibles. Si on prend par exemple des conditions aux limites périodiques pour un volume parallélépipédique : V = LxLyLz, cette quantification s'écrira explicitement : 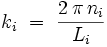 où les entiers
où les entiers 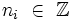 .
.
Voir aussi
Bibliographie
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 3 : Mécanique quantique, éd. MIR, Moscou [détail des éditions]
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 4 : Électrodynamique quantique, éd. MIR, Moscou [détail des éditions]
- Albert Messiah, Mécanique quantique [détail des éditions], tome 2.
- L. I. Schiff, Quantum mechanics (John Wiley & Sons)
- Portail de la physique
Catégorie : Théorie quantique des champs
Wikimedia Foundation. 2010.
