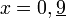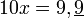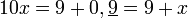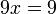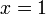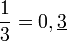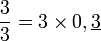- 0.999...
-
Développement décimal de l'unité
Le développement décimal de l'unité ou paradoxe de l'égalité entre 0,9999... et 1 est une curiosité mathématique qualifiée de paradoxe en raison de son caractère contre-intuitif. Il correspond à l'égalité entre les deux écritures du développement décimal de l'unité :
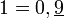, avec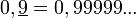 
Sommaire
Première démonstration (via résolution d'une équation)
Soit x un nombre réel.
En multipliant par 10, il s'ensuit que :
On a donc:
Il en résulte que :
Finalement :
Explication
Le côté contre-intuitif de ce raisonnement tient au fait que, dans notre esprit, l'écriture
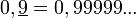correspond à une suite finie de 9 (c'est-à-dire 0,9999...9). Ainsi la multiplication par 10 puis le résultat de la soustraction choque l'esprit et semble faux (qui le serait d'ailleurs si la suite de 9 était finie). Ici elle est juste car 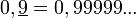correspond à une infinité de 9.Deuxième démonstration (via des fractions)
On pose l'égalité issue de l'algorithme de la division :
En multipliant par 3, il vient :
Il s'ensuit que :
Troisième démonstration (avec une série)
Formalisation de 0,99999…
Pour une démonstration plus rigoureuse, il faut commencer par définir parfaitement ce qu'est 0,999…
En écrivant 0,99999… = 0,9 + 0,09 + 0,009 + … , on définit 0,99999… comme la somme (de tous les termes) d'une série géométrique de premier terme a = 0,9 et de raison q = 1/10.
Ainsi :
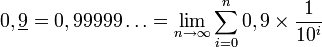
Démonstration par la limite de la série
On peut aisément montrer que la somme des n premiers termes d'une série géométrique de raison q et de premier terme a vaut :
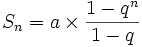
Cette somme tend vers une limite pour n tendant vers l'infini, si et seulement si q est strictement compris entre -1 et 1, et cette limite est alors :
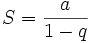
Ici, a = 0,9, q = 1/10, q est plus petit que 1, donc la limite existe et vaut
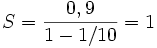
Le paradoxe illustré par l'exemple de l'unité est que tout nombre décimal, c'est-à-dire admettant un développement décimal fini, admet également un développement infini (formé uniquement de 9 à partir d'un certain rang). Le développement fini est l'écriture propre, celui comportant une infinité de 9 est l'écriture impropre. Finalement, ce sont les objets apparemment les plus simples en écriture décimale qui offrent les pires complexités : on croit que 1 est plus simple à écrire en écriture décimale que Pi, et pourtant Pi admet une écriture unique, alors que 1 en admet deux.
Il est important de se souvenir que l'écriture décimale n'est qu'une des multiples manières de représenter un nombre en mathématiques.
Voir aussi
Portail des mathématiques
Catégories : Paradoxe | Nombre 1
Wikimedia Foundation. 2010.
