Coordonées célestes

En astronomie, un système de coordonnées céleste est un système de coordonnées, permettant de déterminer une position dans le ciel, généralement exprimée en notation décimale ou pseudo-sexagésimale (l'unité de base de l'ascension droite étant cependant l'heure sidérale, équivalente à 15°).

Il existe plusieurs systèmes, utilisant une grille de coordonnées projetée sur la sphère céleste, de manière analogue aux systèmes de coordonnées géographiques utilisés à la surface de la Terre. Les systèmes de coordonnées célestes diffèrent seulement dans le choix du plan de référence, qui divise le ciel en deux hémisphères le long d'un grand cercle (le plan de référence du système de coordonnées géographiques est l'équateur terrestre). Chaque système est nommé d'après son plan de référence :

• Système de coordonnées horizontales
• Système de coordonnées horaires
• Système de coordonnées équatoriales
• Système de coordonnées écliptiques
• Système de coordonnées galactiques

Sommaire 1 Conversions 1.1 Des coordonnées horizontales aux coordonnées horaires 1.2 Des coordonnées horaires aux coordonnées horizontales 1.3 Des coordonnées horaires aux coordonnées équatoriales 1.4 Des coordonnées équatoriales aux coordonnées horaires 1.5 Des coordonnées équatoriales vers les coordonnées écliptiques 1.6 Des coordonnées écliptiques vers les coordonnées équatoriales

Conversions

Il existe des formules permettant de passer, de proche en proche, d'un système de coordonnées célestes à un autre système de coordonnées célestes.

Dans le formulaire qui suit, les groupes formés de trois formules doivent être entièrement pris en compte (on ne peut se contenter de respecter 2 formules sur 3), car les fonctions inverses des sinus et des cosinus ne donnent pas nécessairement la bonne solution.

Des coordonnées horizontales aux coordonnées horaires

Connaissant les valeurs respectives Z et h de l'azimuth et de la hauteur, la déclinaison δ et l'angle horaire A_H peuvent être obtenus grâce aux trois formules suivantes :

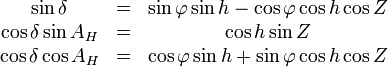
où l'angle φ représente la latitude astronomique du lieu d'observation.

Des coordonnées horaires aux coordonnées horizontales

Connaissant les valeurs respectives A_H et δ de l'angle horaire et de la déclinaison, la hauteur h et l'azimuth Z peuvent être obtenus grâce aux trois formules suivantes :

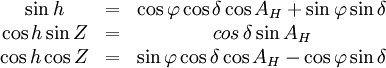
où l'angle φ représente la latitude astronomique du lieu d'observation.

Des coordonnées horaires aux coordonnées équatoriales

Connaissant les valeurs respectives A_H et δ de l'angle horaire et de la déclinaison, l'ascension droite α peut être obtenue très simplement grâce à l'unique formule suivante (la déclinaison reste la même) :

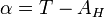
où T représente le temps sidéral au moment de l'observation.

Des coordonnées équatoriales aux coordonnées horaires

Connaissant les valeurs respectives α et δ de l'ascension droite et de la déclinaison, l'angle horaire A_H peut être obtenu très simplement grâce à l'unique formule suivante (la déclinaison reste la même) :

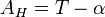
où T représente le temps sidéral au moment de l'observation.

Des coordonnées équatoriales vers les coordonnées écliptiques

Connaissant les valeurs respectives α et δ de l'ascension droite et de la déclinaison, les coordonnées écliptiques ß (latitude) et λ (longitude) peuvent être obtenues grâce aux trois formules suivantes :

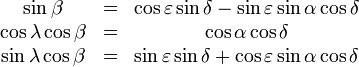
où ε = 23.439281° représente l'obliquité de l'écliptique, c'est-à-dire l'angle que forme le plan de l'équateur terrestre avec le plan de l'orbite terrestre autour du soleil.

Des coordonnées écliptiques vers les coordonnées équatoriales

Connaissant les valeurs respectives λ et ß de la longitude et de la latitude écliptiques, la déclinaison δ et l'ascension droite α peuvent être obtenues grâce aux trois formules suivantes :

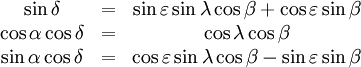
où ε = 23.439281° représente l'obliquité de l'écliptique, c'est-à-dire l'angle que forme le plan de l'équateur terrestre avec le plan de l'orbite terrestre autour du soleil.

• Portail de l’astronomie