Conjugué Isogonal

Sommaire 1 Droites antiparallèles 2 Droites isogonales 2.1 Points sur deux droites isogonales 3 Conjugué isogonal 3.1 Triangle podaire 3.2 Point conjugué isogonal

Droites antiparallèles

Deux couples de droites (d, d') et (Δ, Δ') sont antiparallèles s'ils ont les mêmes directions de bissectrices.

Les angles de droites (d, Δ) et (Δ', d') sont égaux (modulo π).

On dit que d' est antiparallèle à d par rapport à (Δ, Δ').

Quatre points A, B, C et D tels que trois d'entre eux ne sont pas alignés sont cocycliques si et seulement si les droites (AB) et (DC) sont antiparallèles par rapport aux droites (AD) et (BC).

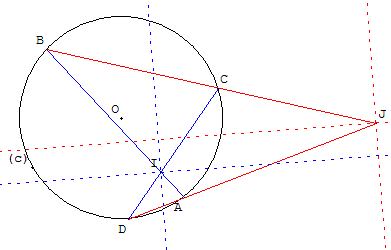
Si deux couples de droites (d, d') et (Δ, Δ') sont antiparallèles et concourants on dit qu'ils isogonaux.

Droites antiparallèles aux côtés d'un triangle
Lorsqu'une droite est antiparallèle à un côté d'un triangle par rapport aux deux autres, on sous-entend assez souvent les deux derniers côtés. On dira : "dans le triangle ABC la droite (d) est antiparallèle à (AB)" à la place de "la droite (d) est antiparallèle à (AB) par rapport à (CA) et (CB)".

D'après Lalesco Trajan - La géométrie du triangle - Jacques Gabay - 2003

Droites isogonales

Deux couples de droites concourantes (d, d') et (Δ, Δ') sont isogonaux s'ils sont antiparallèles.

Ils ont les mêmes bissectrices.

Les angles de droites (d, Δ) et (Δ', d') sont égaux (modulo π).

On dit que d' est isogonale à d par rapport à (Δ, Δ').

Soit d, Δ, Δ' trois droites concourantes. La droite d' symétrique de d par rapport à la bissectrice intérieure de Δ et Δ' est isogonale à d par rapport à (Δ, Δ').

Points sur deux droites isogonales

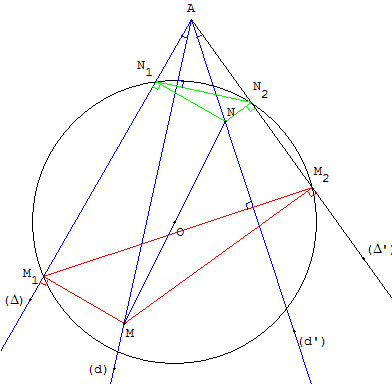
Soit (Δ) et (Δ') deux droites concourantes en A, M et N deux points sur deux droites (d) et (d') concourantes en A.
M₁ et N₁ sont les projections orthogonales de M et N sur (Δ), M₂ et N₂ sur (Δ').
Les deux couples de droites (Δ, Δ') et (d, d') sont isogonaux si et seulement si les points M₁N₁M₂N₂ sont cocycliques.
Le centre O du cercle est le milieu de [MN].
(M₁M₂) est orthogonale à (d), (N₁N₂) est orthogonale à (d')

Conjugué isogonal

Triangle podaire

Soit P un point distinct des sommets du triangle ABC et n'appartenant pas au cercle circonscrit, P₁, P₂, P₃ sont les projections orthogonales de P sur les côtés du triangle.
P₁P₂P₃ est le triangle podaire du point P relativement au triangle ABC. Le cercle circonscrit au triangle P₁P₂P₃ est le cercle podaire.

Point conjugué isogonal

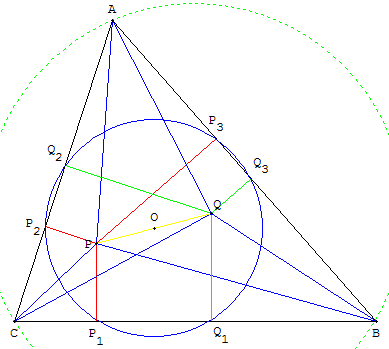
Le conjugué isogonal d'un point P par rapport à un triangle ABC est le point d'intersection des symétriques des droites PA, PB et PC par rapport aux bissectrices des angles du triangle.

Ces trois droites symétriques sont concourantes (cela résulte du théorème de Ceva – version trigonométrique). Si P a pour coordonnées barycentriques 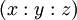alors le conjugué isogonal de P a pour coordonnées barycentriques .

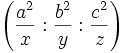Les triangles podaires de deux points isogonaux P et Q sont inscrits dans un même cercle de centre le milieu de [PQ].
Cette propriété permet la construction du point isogonal par l'intermédiaire du cercle podaire.

Exemples :

Les centres des cercles inscrit et exinscrits coïncident avec leurs conjugués isogonaux.

Le centre du cercle circonscrit est le conjugué isogonal de l'orthocentre (d'où des propriétés intéressantes de la droite d'Euler et du cercle de Feuerbach).

Le point de Lemoine est le conjugué isogonal du centre de gravité.

Les deux points de Brocard sont des conjugués isogonaux.

• Portail de la géométrie