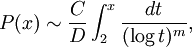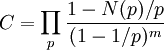Conjecture de bateman-horn

Conjecture de Bateman-Horn

En mathématiques ainsi que dans la théorie des nombres, la conjecture de Bateman-Horn est une vaste généralisation de conjectures telles que la conjecture d'Hardy et Littlewood sur la densité des nombres premiers jumeaux ou leur conjecture sur les nombres premiers de la forme 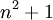$n^2+1\,$ ; c'est aussi un renforcement de l'hypothèse H de Schinzel.

Elle fournit une densité conjecturée pour les entiers positifs auxquels un ensemble donné de polynômes ont tous des valeurs premières. L'ensemble des polynômes 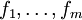$f_1, \dots, f_m\,$ sont m distincts, des polynômes irréductibles à coefficients entiers, tels que le produit f de tous les polynômes f_i possède la propriété de Bunyakovsky : aucun nombre premier p ne divise f(n) pour chaque entier positif n.

Si P(x) est le nombre d'entiers positifs inférieurs à x tel que tous les polynômes ont pour valeur un nombre premier, alors la conjecture est

$P(x) \sim \frac{C}{D} \int_2^x \frac{dt}{(\log t)^m},\,$

où C est le produit sur les nombres premiers p

$C = \prod_p \frac{1-N(p)/p}{(1-1/p)^m}\,$

avec $N (p)$ , le nombre de solutions mod p de 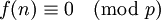$f(n) \equiv 0 \pmod p$ où f est le produit des polynômes f_i, et D est le produit des degrés des polynômes.

Souvent, cette conjecture suppose que les polynômes $f i$ ont le coefficient du terme de plus haut degré positif. C'est une condition non nécessaire si on permet les nombres premiers négatifs (ce qui est raisonnable si vous essayez de formuler la conjecture au-delà du cas classique des nombres entiers), mais en même temps, il est facile de rendre négatif les polynômes si nécessaire pour réduire le cas où les coefficients de terme de plus haut degré sont positifs.

La propriété de Bunyakovsky implique

N (p) < p

pour tous les nombres premiers p, donc chaque facteur dans le produit infini C est positif. Intuitivement, on peut alors espérer que la constante C est elle-même positive, et avec un certain travail, ceci peut être démontré.

Références

Bateman, P. T. and Horn, R. A., “A heuristic asymptotic formula concerning the distribution of prime numbers”, Mathematics of Computation 16 (1962), pp. 363–367

Portail des mathématiques

Ce document provient de « Conjecture de Bateman-Horn ».

Catégories : Théorie analytique des nombres | Conjecture

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture de bateman-horn de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Conjecture De Bateman-Horn — En mathématiques ainsi que dans la théorie des nombres, la conjecture de Bateman Horn est une vaste généralisation de conjectures telles que la conjecture d Hardy et Littlewood sur la densité des nombres premiers jumeaux ou leur conjecture sur… … Wikipédia en Français
Conjecture de Bateman-Horn — En mathématiques ainsi que dans la théorie des nombres, la conjecture de Bateman (en) Horn (non démontrée) est une vaste généralisation de conjectures telles que la conjecture de Hardy et Littlewood sur la densité des nombres premiers… … Wikipédia en Français
Bateman-Horn conjecture — In number theory, the Bateman Horn conjecture is a vast generalization of such conjectures as the Hardy and Littlewood conjecture on the density of twin primes or their conjecture on primes of the form n 2+1; it is also a strengthening of… … Wikipedia
Bateman — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Famille Bateman, Vicomtes de la pairie d Irlande Bateman est un nom de famille notamment porté par : Allan Bateman (né en 1965), joueur de… … Wikipédia en Français
Conjecture de De Polignac — La conjecture de De Polignac est une conjecture portant sur la théorie des nombres. Elle fut énoncée par Alphonse de Polignac en 1849[1]. La formulation initiale est la suivante : Tout nombre pair est égal à la différence de deux nombres… … Wikipédia en Français
Robert Bateman — Bateman Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Bateman est un nom de famille notamment porté par : James Bateman (1811 1897), botaniste britannique. Robert Bateman (artiste)… … Wikipédia en Français
Polignac's conjecture — In number theory, Polignac s conjecture was made by Alphonse de Polignac in 1849 and states: For any positive even number n, there are infinitely many prime gaps of size n. In other words: There are infinitely many cases of two consecutive prime… … Wikipedia
Nombre premier — 7 est un nombre premier car il admet exactement deux diviseurs positifs. Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui même). Cette définition exclut 1, qui n a… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste Des Conjectures Mathématiques — Ce qui suit est une liste de conjectures mathématiques, contenues dans les pages de Wikipedia. Elles sont divisées en quatre sections, en accord avec leur état en 2006. Voir aussi : La conjecture d Erdős, qui liste les conjectures de Paul… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Conjecture de bateman-horn