Conjecture de Erdős-Burr

Soit G un graphe simple. Il découle du théorème de Ramsey qu'il existe un entier r(G) minimal, le nombre de Ramsey de G, tel que tout graphe complet d'au moins r(G) sommets dont les arêtes sont coloriées en rouge et bleu contienne une copie monochromatique de G.

En 1973, Erdős et Burr ont proposé la conjecture suivante:

Pour tout entier p, il existe une constante c_p telle que tout graphe G ayant n sommets et dont tous les sous-graphes ont un degré minimum au moins p ait son nombre de Ramsey borné par .

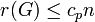Cette conjecture a été vérifiée dans certains cas particuliers:

• pour les graphes de degré maximal borné;
• pour les graphes p-arrangeables et, en particulier, les graphes planaires et les graphes sans subdivisions de K_p;
• pour les graphes subdivisés.

Références

• N. Alon (1994). Subdivided graphs have linear ramsey numbers. J. Graph Theory 18(4), 343–347.
• S.A. Burr and P. Erdős (1975). On the magnitude of generalized Ramsey numbers for graphs. Colloquia Mathematica Societatis Janos Bolyai 10 Infinite and Finite Sets 1, 214–240.
• G. Chen and R.H. Schelp (1993). Graphs with linearly bounded Ramsey numbers, J. Combin. Theory Ser. B 57(1), 138–149.
• V. Chvátal, V. Rödl, E. Szemerdi, and W.T. Trotter Jr. (1983). The Ramsey number of a graph with bounded maximum degree, J. Combin. Theory Ser. B 34(3), 239–243.
• N. Eaton (1998). Ramsey numbers for sparse graphs, Discrete Maths 185, 63–75.
• R.L. Graham, V. Rödl, and A. Rucínski (2000). On graphs with linear Ramsey numbers, Journal of Graph Theory 35, 176–192.
• R.L. Graham, V. Rödl, and A. Rucínski (2001). On bipartite graphs with linear Ramsey numbers, Paul Erd¨os and his mathematics, Combinatorica 21, 199–209.
• Yusheng Li, C.C. Rousseau, and L. Soltés (1997). Ramsey linear families and generalized subdivided graphs, Discrete Mathematics, 269–275.
• V. Rödl and R. Thomas (1991). Arrangeability and clique subdivisions, The mathematics of Paul Erdös (R.L. Graham and J. Nešetřil, eds.), Springer, pp. 236–239.

• Portail des mathématiques