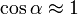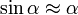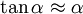Conditions de gauss
- Conditions de gauss
-
Approximation de Gauss
L'approximation de Gauss (d'après le physicien allemand Carl Friedrich Gauss) est l'approximation linéaire de l'optique géométrique[1] obtenue lorsque les angles d'incidence des rayons sont faibles et que le point d'incidence est proche de l'axe optique. Les écarts à cette approximation (rencontrés notamment dans les instruments d'optique travaillant en « grand angle ») sont appelés aberrations géométriques.
L'ensemble des conditions menant à l'approximation de Gauss est appelé conditions de Gauss.
Conséquences mathématiques
L'approximation des petits angles permet, au premier ordre, la linéarisation des fonctions trigonométriques de base :
Notes et références de l'article
- ↑ José-Philippe Pérez, Optique : Fondements et applications, [détail des éditions], 5e édition, page 28.
Voir aussi
Articles connexes
 Portail de la physique
Portail de la physique
Catégorie : Optique géométrique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Conditions de gauss de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Conditions de Gauss — Approximation de Gauss L approximation de Gauss (d après le physicien allemand Carl Friedrich Gauss) est l approximation linéaire de l optique géométrique[1] obtenue lorsque les angles d incidence des rayons sont faibles et que le point d… … Wikipédia en Français
Gauss — Carl Friedrich Gauss « Gauss » redirige ici. Pour les autres significations, voir Gauss (homonymie). Carl Friedrich Gauss … Wikipédia en Français
GAUSS (C. F.) — L’œuvre du mathématicien allemand Carl Friedrich Gauss (né à Brunswick, mort à Göttingen) est un monument d’une ampleur et d’une richesse sans égale: non seulement il y a Gauss mathématicien, mais il y a aussi le calculateur, le géodésien,… … Encyclopédie Universelle
Conditions De Kuhn-Tucker — Pour les articles homonymes, voir condition. En mathématiques, les conditions de Kuhn Tucker ou conditions de Karush Kuhn Tucker permettent de résoudre des problèmes d optimisation sous contraintes non linéaires d inégalité. Soient :… … Wikipédia en Français
Conditions de Karush-Kuhn-Tucker — Conditions de Kuhn Tucker Pour les articles homonymes, voir condition. En mathématiques, les conditions de Kuhn Tucker ou conditions de Karush Kuhn Tucker permettent de résoudre des problèmes d optimisation sous contraintes non linéaires d… … Wikipédia en Français
Conditions de kuhn-tucker — Pour les articles homonymes, voir condition. En mathématiques, les conditions de Kuhn Tucker ou conditions de Karush Kuhn Tucker permettent de résoudre des problèmes d optimisation sous contraintes non linéaires d inégalité. Soient :… … Wikipédia en Français
Gauss pseudospectral method — The Gauss Pseudospectral Method (abbreviated GPM ) is a direct transcription method for discretizing a continuous optimal control problem into a nonlinear program (NLP). The Gauss pseudospectral method differs from several other pseudospectral… … Wikipedia
Gauss' principle of least constraint — The principle of least constraint is another formulation of classical mechanics enunciated by Carl Friedrich Gauss in 1829.The principle of least constraint is a least squares principle stating that the true motion of a mechanical system of N… … Wikipedia
Gauss–Newton algorithm — The Gauss–Newton algorithm is a method used to solve non linear least squares problems. It can be seen as a modification of Newton s method for finding a minimum of a function. Unlike Newton s method, the Gauss–Newton algorithm can only be used… … Wikipedia
Conditions de Kuhn-Tucker — Pour les articles homonymes, voir condition. En mathématiques, les conditions de Kuhn Tucker ou conditions de Karush Kuhn Tucker permettent de résoudre des problèmes d optimisation sous contraintes non linéaires d inégalité. Soient :… … Wikipédia en Français