Aberrations en optique des particules chargées

Les aberrations en optique des particules chargées sont l'équivalent des aberrations en optique photonique. L'étude des aberrations des lentilles électroniques est presque aussi vieille que le microscope électronique^[1]. Il n'y a pas de différences entre les aberrations géométriques de l'optique photonique ou de l'optique des particules chargées. L'aberration chromatique est assez proche dans les deux disciplines, mais la longueur d'onde de l'optique photonique est remplacée par la variation relative d'énergie. Du fait que l'existence de la charge électrique, certaines aberrations seront la conséquence de la répulsion coulombienne et seront appelées « aberrations de charge d'espace » pour certaines d'entre elles et « aberrations coulombiennes stochastiques » pour d'autres.

L'optique électronique est une restriction de l'optique des particules chargées au cas des électrons. Chaque fois que la masse n'intervient pas dans la description d'une aberration, il est cependant courant de la décrire comme s'il s'agissait d'un électron.

Sommaire

1 Historique
2 Optique gaussienne, plan de Gauss
3 Définition canonique
4 Dans les systèmes à symétrie de révolution
5 Calcul des aberrations géométriques et chromatiques
6 Aberrations de charge d’espace
7 Notes et références
8 Voir aussi
- 8.1 Bibliographie
- 8.2 Articles connexes

Historique

Les premiers calculs des coefficients d'aberration ont été effectués dès le début des années 1930^[1] par Scherzer^[2] qui utilisait la méthode des trajectoires paraxiales et par Glaser qui a introduit la méthode de l'eikonal ^[3]. Pendant les années 1930, les aberrations des lentilles circulaires sont étudiées intensivement et plusieurs auteurs aboutissent à des formules concernant les différents coefficients d'aberrations. Notamment Scherzer parvient à démontrer un théorème^[4] particulièrement intéressant pour la résolution des microscopes électroniques: Quel que soit le dessin d'une lentille, électrostatique ou magnétique, son aberration sphérique est toujours positive^[1].

Dans les années 1940, des auteurs parmi lesquels on retrouve Scherzer, calculent les aberrations des quadrupoles et proposent un certain nombre de méthodes pour annuler leur aberration sphérique^[1].

C'est à la fin des années 1940 que des auteurs commencent à s'attaquer au problème des aberrations du second ordre dans des dispositifs courbes tels que le secteur magnétique ou le secteur électrostatique^[5]: Pour les secteurs magnétiques, Hintenberger en 1948^[6], puis Kerwin, Tasman, Boerboom et finalement Enge en 1967^[7]. Pour les secteurs électrostatiques, Ewald et Liebl en 1957^[8], Wollnick en 1965^[9].

Optique gaussienne, plan de Gauss

Définition canonique

Dans un très grand nombre de systèmes d'optique électronique ou ionique, il est possible de privilégier une trajectoire médiane, paramétrée en z, distance le long de la trajectoire et une tension d'accélération nominale E. La trajectoire médiane est généralement l'axe de symétrie mécanique des instruments que l'on appellera axe principal. Certaines parties de cet axe sont droites, mais d'autres parties peuvent être courbes, par exemple, dans les secteurs électrostatiques ou magnétiques utilisés dans les spectromètres de masse. On peut alors considérer n'importe quel système optique comme une fonction de transformation des trajectoires entre un plan d'entrée situé à $z i$ , où l'indice "i" signifie « input » et un plan de sortie situé à $z o$ , où l'indice "o" signifie « output ». Ces indices sont un peu malheureux, car ils entraînent une confusion avec « image » et « objet », mais c'est ainsi qu'ils sont définis dans la littérature^[10].

Dans un plan donné, perpendiculaire à l'axe principal, repéré par des axes OX et OY, n'importe quelle trajectoire électronique ou ionique peut être caractérisée par un vecteur (x, y, a, b, m, e) où

(x, y) sont les coordonnées de la particule
(a, b) sont les angles d'ouvertures respectifs par rapport à l'axe principal OZ dans les plans ZOX et ZOY
e=dE/E est la différence relative entre la tension d'accélération de la particule et la tension d'accélération nominale E .
m=dM/M est la différence relative entre la masse de la particule et la masse nominale M.

Chaque composante du vecteur de sortie peut alors s'exprimer comme une fonction des composantes du vecteur d'entrée et peut être approximé par une Série de Taylor.

$x_O = (x/x) * x_i + (x/y) * y_i + (x/a) * a_i + (x/b) * b_i + (x/m) * m + (x/e) * e + (x/xx) * x_i^2 ... + (x/aa) * a_i^2 + (x/ae) * a_i * e +.... + (x/aaa) * a_i^3 ...$

$y_O = (y/x) * x_i + (y/y) * y_i + (y/a) * a_i + (y/b) * b_i + (y/m) * m + (y/e) * e + (y/xx) * x_i^2 + (y/aa) * a_i^2 + (y/ae) * a_i * e +.... + (y/aaa) * a_i^3 ...$

$a_O = (a/x) * x_i + (a/y) * y_i + (a/a) * a_i + (a/b) * b_i + (a/m) * m + (a/e) * e + (a/xx) * x_i2 ... + (a/aa) * a_i^2 + (a/ae) * a_i * e +.... + (a/aaa) * a_i^3 ...$

$b_O = (b/x) * x_i + (b/y) * y_i + (b/a) * a_i + (b/b) * b_i + (b/m) * m + (b/e) * e + (b/xx) * x_i^2 ... + (b/aa) * a_i^2 + (b/ae) * a_i * e +.... + (b/aaa) * a_i^3 ...$

Il doit être clair que (x/ae) ou (a/x) ou y(bbb) désignent des coefficients. L'ensemble complet de ces coefficients est parfois appelé la Matrice de Transfert. Il faut comprendre que dans la mesure où on l'on connait les coefficients de chaque constituant du système, il est possible de calculer facilement les coefficients de l'ensemble du système.

On peut donner à chaque coefficient une signification physique. Par exemple (x/x) et (y/y) sont des grandissements alors que (a/x) et (b/y) sont des inverses de distance focale. On peut aussi signaler que (x/m) est un coefficient de dispersion en masse et (x/e) un coefficient de dispersion en énergie.

Dans un certain nombre de cas particuliers, on peut démontrer que certains coefficients sont nécessairement nuls pour des raisons de symétrie. Par exemple, une lentille électrostatique pourvue d'une symétrie de révolution aura ses coefficients du second ordre (a/xx), (a/yy), (a/xy) etc... égaux à zéro.

Les termes du deuxième et du troisième ordre (et bien sûr, au-delà) sont considérés comme des effets parasites, non désirés, dans la plupart des systèmes optiques. On les appelle des « aberrations ». Certains dispositifs, par exemple des hexapoles, qui produisent un certain type d'aberrations - dans le cas des hexapoles, ce sont des aberrations du deuxième ordre, sont inclus dans des systèmes optiques en vue d'annuler des aberrations produits par d'autres dispositifs indispensables dans l'instrumentation considérée? Par exemple, les secteurs magnétiques qui sont utilisés pour leur dispersion en masse, produisent également des termes parasites (x/aa), (x/ae)...

Dans les systèmes à symétrie de révolution

Aberrations géométriques du troisième ordre

Dans un système à symétrie de révolution, c'est-à-dire un système constitué de lentilles électrostatiques et de lentilles magnétiques comme le sont les microscopes électroniques, il est naturel de travailler en coordonnées cylindriques en exprimant la position de la particule à l'aide de son rayon vecteur r et de son azimut $φ$ . On travaillera alors avec les variables complexes u et v et w définis par ^[11]

$\textstyle u = x_O +i y_0 = r_O * e^{i\phi_O}$

$\bar u\ = x_O -i y_0 = r_O *e^{-i\phi_O}$

$\textstyle w = x_i +i y_i = r_i * e^{i\phi_i}$

La symétrie de révolution conduit à éliminer les termes d'ordre pair, à commencer par le second ordre. Elle impose aussi, pour tous les termes du troisième ordre de type $\textstyle uuv, \ v^2 \bar v , \ \bar v^3$ , à ne conserver que ceux dont la phase est $φ$ ^[11]:

$w = \left( \bold A + i \bold A'\right)\ v^2 \bar v\ + \left( \bold B + i \bold B'\right) u^2 \bar v\ + \left( \bold C + i \bold C'\right)\ u \bar u\ v + \left( \bold D + i \bold D'\right) \bar u\ v^2 + \left( \bold E + i \bold E'\right) u v\bar v\ + \left( \bold F + i \bold F'\right) u^2\bar u\$

Par ailleurs Par des considérations de symétrie, et en vertu du théorème de Malus Dupin qui impose^[11]:

$Im(\frac{\delta w}{\delta v}) = 0$

on arrive à simplifier et à supprimer un certain nombre de termes:

$\bold A' = \bold C' = 0$

$\bold E = 2\bold D$

$\bold E' = -2\bold D'$

Ce qui conduit à une relation valide aussi bien pour les lentilles magnétiques que pour les lentilles électrostatiques^[11]

$w = \bold A\ v^2 \bar v\ + \left( \bold B + i \bold B'\right) u^2 \bar v\ + \bold C\ u \bar u\ v + \left( \bold D + i \bold D'\right) \bar u\ v^2 + 2\left( \bold D - i \bold D'\right) u v\bar v\ + \left( \bold F + i \bold F'\right) u^2\bar u\$

Mais dans le cas des lentilles électrostatiques, on peut mettre à profit le fait qu'aucune force ne peut amener un électron à quitter un plan méridien^[11].

$\bold B' = \bold D' = \bold F' = 0$

A est connu comme le coefficient d'aberration sphérique^[12]
D est connu comme le coefficient de coma^[12]
D est connu comme le coefficient de coma anisotropique^[12]
B est connu comme le coefficient d'astigmatisme^[12]
B' est connu comme le coefficient d'astigmatisme anisotropique^[12]
C est connu comme le coefficient de courbure de champ^[12] * F est connu comme le coefficient de distorsion^[12]
F' est connu comme le coefficient de distorsion anisotropique^[12]

Toutes ces aberrations géométriques sont discutées ci-dessous.

Discussion détaillée des différentes aberrations géométriques

Article détaillé : Aberration géométrique.

On peut définir de façon canonique 5 types d'aberrations géométriques: l'aberration sphérique, coma, la courbure de champ, l'astigmatisme et la distorsion.

Aberration sphérique

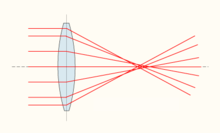Réprésentation de l'aberration sphérique.

L'aberration sphérique est une aberration du troisième ordre qui traduit le fait qu'une lentille, qu'elle soit magnétique ou électrostatique, est toujours plus convergente pour les trajectoires périphériques que pour les trajectoires centrales. Le coefficient d'aberration sphérique $C s$ est défini par la relation:^[13]

r s = C s θ 3 M

où $r s$ est la distance à l'axe, dans le plan image de Gauss de la trajectoire associé à l'angle d'ouverture $θ$ et M étant le grandissement du système optique considéré.

La section du faisceau n'est pas minimale au plan de Gauss, mais à un plan voisin. Dans ce plan, la section du faisceau est appelée disque de moindre confusion $d s, m i n$ dont on peut montrer qu'il est égal à^[13]: Pour un faisceau ayant un angle d'ouverture $α 0$ , le faisceau n'est pas focalisé en un point, mais en un disque dans le plan image, appelé disque de moindre confusion de diamètre minimum $d s, m i n$ :^[13]

$d_{s,min} = \frac{1}{2} C_s \alpha_0^3$

$α 0$ , étant l'angle d'ouverture du faisceau.

Scherzer a démontré par un théorème qui porte son nom que l'aberration sphérique était toujours positive dans un système à symétrie de révolution. On a cependant imaginé à la fin des années soixante-dix de contourner le théorème se Scherzer par des systèmes qui ne sont pas à symétrie de révolution et qui nécessitent de faire passer le faisceau hors d'axe. Ces systèmes consistent en un certain nombre d'étages de multipoles. Leur réglage nécessitant des algorithmes sophistiqués, ce n'est que depuis le début des années 2000 qu'ils ont pu être intégrés dans des microscopes électroniques commercialisés.

Astigmatisme

L'astigmatisme a pour effet de ne pas faire converger les rayons issus d'un même point suivant leurs directions initiales. En considérant une focale $F m$ suivant le plan méridien, et l'autre $F s$ suivant le plan sagittal^[14], on observe une différence de focale $Δ f a = F m - F a$ . De cette différence résulte un cercle de moindre confusion de diamètre $d a$ donné par :^[15]

d a = Δ f a α 0

Dans le cas d'une lentille, l'origine de cette aberration vient des variations de champs dues aux inhomogénéités de la lentille ou des contaminations éventuelles sur la surfaces des diaphragmes et de l'échantillon. L'astigmatisme est corrigé par une paire de stigmateurs, décalés de 45°.

Aberrations chromatiques

En pratique, le faisceau électronique n'est pas complètement monochromatique, c'est-à-dire que la longueur d'onde (ou l'énergie) varie faiblement d'un électron à l'autre. La focalisation des lentilles magnétiques magnétique dépendant fortement de l'énergie des électrons, il en résulte une succession de foyers qui sont compris entre le foyer pour les électrons les plus lents $F l$ et celui pour les plus rapides $F r$ . Cette différence $Δ f c = F l - F r$ et la constante d'aberration chromatique caractérise le cercle de moindre confusion dont le diamètre $d c$ est donnée par :

$d_c = \frac{1}{2} \Delta f_c \alpha_0$

Cette aberration est dite d'ordre un, car elle est proportionnelle à l'ouverture angulaire $α 0$ .

Calcul des aberrations géométriques et chromatiques

Aberrations de charge d’espace

Si le faisceau de particules chargées est très intense, les phénomènes de répulsion coulombienne internes au faisceau entre charges électriques de même signe ne sont pas négligeables et conduisent à des aberrations dites de charge d'espace qui peuvent se corriger, en première approche par une refocalisation de la lentille objectif dans la mesure où les forces de répulsion ont un aspect continu et ne dépendent que de la position d'un point considéré.

Les effets sur les trajectoires résultant de répulsion coulombienne stochastique, autrefois appelées effet Boersch, sont, elles, incorrigeables.

Notes et références

↑ ^{a, b, c et d} (en) P. W. Hawkes, E. Kasper, Principles of Electron Optics, Academic Press, 1988, p. 299-302
↑ O.Scherzer, Z. Physik 80, 193-202 (1933)
↑ W.Glaser, Z. Physik, 81, p.647-686
↑ O.Scherzer, Z.Physik, 101, 593-603
↑ Pierre Grivet, Electron optics, Tome 1, édition anglaise de 1972, p.349 et 367-368
↑ Hintenberger, Z.Naturforsch., "a, 125 et 669 (1948)
↑ Harald A.Enge, Deflecting Magnets, dans Focusing of charged particles, ed. by Albert Septier, Academic Press, 1967, p.203-264
↑ H.Ewald et H.Liebl, Z.Naturforsch. 12a. 28 (1957)
↑ Hermann Wollnik, Electrostatic Prisms, dans Focusing of charged particles, ed. by Albert Septier, Academic Press, 1967, p.163-202
↑ Par exemple, les articles de Wollnick et Enge dans Focusing of charged particles, ed. by Albert Septier, Academic Press, 1967, p.163-202 et p.203-264
↑ ^{a, b, c, d et e} Grivet, p.156-158
↑ ^{a, b, c, d, e, f, g et h} Grivet, p.159-162
↑ ^{a, b et c} Reimer 1993, p. 37-38
↑ plan défini perpendiculaire au plan méridien,
↑ Reimer 1993, p. 40

Voir aussi

Bibliographie

(en) P. W. Hawkes et E. Kasper, Principles of Electron Optics, Academic Press, 1988, p. 299. (ouvrage de référence pour l'optique électronique depuis 1988, mais un peu difficile à lire. L'optique des systèmes courbes, à la base de l'optique ionique, n'y est qu'effleuré.)
(en) Pierre Grivet, Electron optics, Tome 1, première édition anglaise, Pergamon press 1965, deuxième édition, 1972. (ouvrage classique depuis la fin des années 1950)
Maurice Cotte, Recherches sur l'optique électronique, Ann. Phys. Paris, 10, 333, 73 p. (première monographie en français)

Systèmes à axe courbé

(en) Hermann Wollnik, Optics of charged particles, Academic press, 1987 (Ciblé vers les gros accélérateurs)
Hermann Wollnik, Electrostatic Prisms, dans Focusing of charged particles, ed. by Albert Septier, Academic Press, 1967, p. 163-202 (pour les secteurs électrostatiques)
(en) Harald A.Enge, Deflecting Magnets, dans Focusing of charged particles, ed. by Albert Septier, Academic Press, 1967, p. 203-264 (Pour les secteurs magnétiques)

Regardez d'autres dictionnaires:

Optique des particules chargees — Optique des particules chargées L optique des particules chargées est l ensemble des techniques destinées à dévier un faisceau électronique ou ionique. Le terme « optique » renvoie à l analogie entre un rayon électronique et un rayon… … Wikipédia en Français
Optique des particules chargées — L optique des particules chargées est l ensemble des techniques destinées à dévier un faisceau électronique ou ionique. Le terme « optique » renvoie à l analogie entre un rayon électronique et un rayon lumineux, avec notamment la notion … Wikipédia en Français
Optique ionique — Optique des particules chargées L optique des particules chargées est l ensemble des techniques destinées à dévier un faisceau électronique ou ionique. Le terme « optique » renvoie à l analogie entre un rayon électronique et un rayon… … Wikipédia en Français
Optique électronique — Optique des particules chargées L optique des particules chargées est l ensemble des techniques destinées à dévier un faisceau électronique ou ionique. Le terme « optique » renvoie à l analogie entre un rayon électronique et un rayon… … Wikipédia en Français
OPTIQUE - Optique électronique — L’optique électronique ou plus généralement l’optique corpusculaire s’intéresse aux trajectoires d’électrons libres accélérés, et à tous les procédés permettant de guider ces particules dans un espace où règne un vide poussé. On peut en effet se… … Encyclopédie Universelle
OPTIQUE — ON PEUT, semble t il, définir l’optique comme l’étude des moyens de transmission des informations par la lumière, ces informations portant soit sur la forme, la luminosité, la couleur, la position d’objets dont on obtient des images, soit sur… … Encyclopédie Universelle
Aberration (Optique) — Les aberrations optiques sont un ensemble de phénomènes qui font qu une image créée par un système optique n est pas conforme à la réalité. Citons : l aberration chromatique, phénomène qui disperse les couleurs du fait d une variation de l… … Wikipédia en Français
Aberration optique — Aberration (optique) Les aberrations optiques sont un ensemble de phénomènes qui font qu une image créée par un système optique n est pas conforme à la réalité. Citons : l aberration chromatique, phénomène qui disperse les couleurs du fait d … Wikipédia en Français
Aberration (optique) — Les aberrations optiques sont un ensemble de phénomènes qui font qu une image créée par un système optique n est pas conforme à la réalité. Citons : l aberration chromatique, phénomène qui disperse les couleurs du fait d une variation de l… … Wikipédia en Français
PARTICULES (ACCÉLÉRATEURS DE) — Les modèles et théories qui synthétisent notre compréhension actuelle de la matière et de ses constituants élémentaires – molécules, atomes, particules – ont été confrontés à une multitude d’observations expérimentales. Pour réaliser ces… … Encyclopédie Universelle