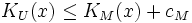Complexité de kolmogorov

La complexité de Kolmogorov (nommée d'après le mathématicien Andreï Kolmogorov), nommée aussi complexité aléatoire, ou complexité algorithmique, est une fonction (plus précisément un ensemble de fonctions) permettant d'évaluer la complexité de calcul d'un nombre ou d'une suite.

Sommaire 1 Présentation informelle 2 Propriétés 3 Voir aussi 3.1 Articles connexes 3.2 Références

Présentation informelle

Considérons une machine informatique M pouvant exécuter des programmes. On dit que cette machine est universelle lorsqu’elle peut émuler n'importe quelle autre machine informatique. La machine de Turing universelle en est un exemple.

On note P_M l'ensemble des programmes écrits pour la machine M. Pour un programme 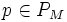, on note l(p) sa longueur en nombre d’instructions pour la machine M et s(p) sa sortie. La complexité de Kolmogorov K_M(x), ou complexité algorithmique, d’une suite x = (x_i)_i pour une machine M est définie par :

.

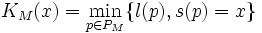C’est donc la longueur du plus petit programme écrit pour la machine M qui génère la suite x. Une suite constante a une complexité faible car les programmes qui la génèrent peuvent être très courts.

Reste à savoir dans quelle mesure la fonction K_M(x) dépend de la machine M, car on peut tout à fait imaginer une machine possédant des instructions simples pour générer certaines suites complexes. La réponse est la suivante : il existe une machine universelle U (souvent qualifiée d'additivement optimale) telle que pour toute machine M il existe une constante c_M vérifiant pour toute suite x l'inégalité

Intuitivement, c_M est la longueur d'un interpréteur (ou d'un émulateur), écrit pour la machine U, du langage utilisé par la machine M. On parle alors d’universalité de la complexité de Kolmogorov, en ce sens qu'elle ne dépend pas, à une constante additive près, de la machine considérée.

Une suite peut alors être considérée comme d’autant plus « aléatoire » que sa complexité est grande par rapport à sa taille. De ce point de vue, les décimales des nombres π, e ou 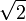ne sont pas vraiment aléatoires puisqu'il existe des algorithmes très simples pour les calculer.

Propriétés

La complexité de Kolmogorov n'est pas calculable. En d'autre termes il n'existe pas de programme informatique qui prenne en entrée s et renvoie K(s). Raisonnons par l'absurde et supposons qu'une telle fonction Kolmo existe; la taille de cette fonction (nombre de caractères) est connue et égale à k. On pourrait alors écrire l'algorithme suivant:

  n :=1 
     Tant que Kolmo(n)<k+100 faire:
        n:=n+1
     Fin du Tant que
  écrire n

Ainsi cet algorithme écrit le plus petit nombre à avoir une complexité de Kolmogorov supérieure à k+100 (ce nombre existe nécessairement car il n'y a qu'un nombre fini de programmes de tailles plus petite que k+100 et il y a une infinité de nombres entiers naturels).

Mais l'algorithme ci-dessus s'écrit justement avec moins de k+100 caractères : il est donc de complexité inférieure à k+100, or il écrit justement un nombre de complexité supérieure à k+100, ce qui est absurde.

Donc il n'existe pas de fonction qui calcule la complexité de Kolmogorov.

Voir aussi

Articles connexes

• Machine de Turing
• Théorie algorithmique de l'information
• Suite aléatoire

Références

Une partie de cet article (ou d'une version antérieure) est adaptée de [1], sous GFDL.