Comparaisons Par Paires

De nombreux travaux théoriques ont démontré que les relations complexes entre divers éléments indépendants pouvaient être étudiées au moyen de comparaisons analogiques binaires, c'est-à-dire, en les comparant deux à deux. En effet, une telle démarche permet de décomposer le problème posé en réduisant la masse d’informations à acquérir et à intégrer d’une part, en concentrant la réflexion du répondant sur ses composantes essentielles, d’autre part.

Sans entrer dans des détails mathématiques complexes, le calcul matriciel représente un environnement simple et efficace, disposant de tous les outils nécessaires pour réaliser avec efficacité de telles comparaisons. Le recours à un ordinateur pour effectuer, au moyen d’un logiciel approprié, les phases d’acquisition, de calcul et de contrôle en rend aujourd’hui la pratique particulièrement aisée pour tous les néophytes.

Il s’agit en effet, de comparer en termes de ratios deux à deux, compte tenu d’un but poursuivi B et au moyen d’un questionnement approprié q, un ensemble d’éléments E1 à En, chaque élément prenant automatiquement et logiquement le ratio 1 / 1 = 1 ou 1 x 1 = 1, lorsque comparé à lui-même au sein d'une matrice.

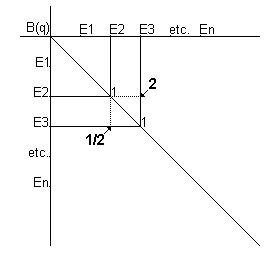
En pratique, l’intersection de chaque ligne et de chaque colonne de cette matrice figure le ratio existant entre les deux éléments en vis à vis, tel qu’indiqué par le répondant. De part et d’autre de la diagonale comportant nécessairement des ratios égaux à 1, doivent donc logiquement figurer des ratios réciproques : si le ratio E3 / E2 est égal à 2, alors le ratio E2 / E3 doit être égal à ½.

A l’appui, prenons l’exemple suivant :

• B = choix d’une voiture • q = quelle voiture préférez-vous ? • E1 = voiture A • E2 = voiture B

Si la voiture A est préférée 2 fois plus que la voiture B, alors, la voiture B est préférée 2 fois moins (soit ½) que la voiture A. Vous constaterez donc qu’il suffit en pratique de ne renseigner qu’une demi matrice pour obtenir des résultats complets.

Dans ces conditions, le nombre total N de comparaisons à effectuer pour remplir totalement la matrice est donné par la relation très simple :

N = (n² - n) / 2

Où n représente le nombre d’éléments à com- parer, ou, en d’autres termes, le rang de la matrice.

Tant pour des raisons de praticité que de capacités humaines, le nombre n d’éléments appartenant à un même cycle de comparaisons par paires sera volontairement limité à 7 ou 8. Ceci garantit un nombre acceptable d’interrogations d’une part, une concentration en amont de la réflexion sur les principaux éléments constitutifs de la décision, d’autre part.

Vous noterez qu’une telle approche est totalement indépendante de la nature de l’information traitée et permet d’aborder tous les sujets, quels qu’ils soient, y compris ceux faisant appel à des mesures numériques :

• B = choix d’une voiture • Q = quelle voiture consomme le moins ? • E1 = voiture A • E2 = voiture B

Les consommations peuvent ici être aisément obtenues sur la notice des constructeurs concernés et traduites sous la forme de ratios exacts ou encore appréciées approximativement.

Quelles que soient les informations à l’origine de la réponse, elles sont interprétées et traduites par le répondant pour restituer le ratio effectif existant entre deux éléments, au sein d’un même référentiel relatif, constitué pour l’occasion.

A l’issue du processus de renseignement des ratios, une synthèse est effectuée au moyen de calculs élémentaires, visant à restituer les pondérations globales obtenues par chaque élément de telle sorte que le résultat final prenne la forme :

Voiture A = 45.2 % Voiture B = 22.3 % Voiture C = 32.5 %

Liens externes & internes

• Aide à la décision
• Recherche opérationnelle

Ouvrages

• Thomas L. Saaty. Décider face à la complexité - Editions EME. 1984.
• Jean-Michel Grand. Le Décideur Chrono - Editions Paulo-Ramand. 2006.

• Portail de l’informatique