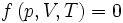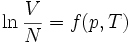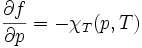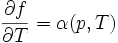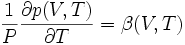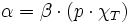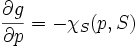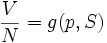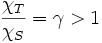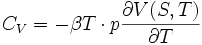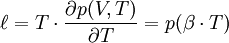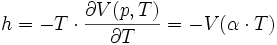- Coefficient thermoélastique
-
Formules de thermodynamique
En thermodynamique moderne, les fonctions d'état caractéristiques corps pur peuvent être exprimées au moyen de nombreuses relations.
Les fonctions d'état sont : la pression p, la température T, le volume V, l'énergie interne U, l'entropie S, l'enthalpie H, l'énergie libre F et l'enthalpie libre G.
Entre ces fonctions et leurs dérivées partielles, on peut établir des dizaines de formules : il existe 28 expressions des fonctions d'état, donc 56 dérivées partielles.
En réalité, seules certaines ont un intérêt scientifique et pratique.
Sommaire
Thermoélasticité
La première formule importante est intrinsèquement liée à l'équation d'état :
Elle peut être interprétée comme l'équation d'une surface dans un espace vectoriel à trois dimensions.
L'habitude est de définir le plan tangent à la surface en un point A (appelé un « état A »). Par exemple, si on considère la quantité facilement mesurable :
On peut en déduire les 2 coefficients thermoélastiques du gradient :
Le nombre χT, positif, est appelé « coefficient thermoélastique de compressibilité isotherme », homogène à l'inverse d'une pression, reliée en physique statistique aux fluctuations de pression,
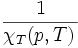 (en pascals).
(en pascals).Le nombre α est appelé « coefficient thermoélastique de dilatation isobare », qui est souvent positive, avec des exceptions notables comme l'eau liquide entre 0 °C et 4 °C et le bismuth.
On définit aussi le coefficient β :
appelé « coefficient thermoélastique d'augmentation relative de pression isochore » (à préférer à « dilatation isochore »).
Il existe une relation entre β, α et χT :
- α est lié à la loi de Gay-Lussac ;
- β est lié à la loi de Charles ;
- χT est lié à la loi de Mariotte et aux expériences d'Amagat.
On définit la compressibilité adiabatique :
avec
On démontre alors la formule de Reech :
Relations de Mayer
On définit l'enthalpie :
- H = U + pV
Cette relation suggère un lien entre Cp, CV et les coefficients thermoélastiques. La relation de Mayer l'établit.
Réciproquement, la formule de Reech suggère une autre relation du même type :
Cette relation fait intervenir P = ƒ(S,T), qui est plus difficile à obtenir.
De même :
À entropie constante, le volume V peut diminuer quand la température T augmente (si α T est positif), ce qui justifie le signe négatif.
Il existe des relations analogues à celle de Mayer pour les coefficients de réponse à la pression, c’est-à-dire pour χT et χS.
Relations de Clapeyron
Le « coefficient de chaleur latente de dilatation », noté ℓ, vaut :
Le « coefficient de chaleur latente de compression », noté h, vaut :
Ces relations ont été trouvées très tôt[réf. nécessaire]. Leur vérification expérimentale par Thomson et Joule constitueront en fait le premier test démontrant une contradiction dans la « théorie du calorique », appelant la construction d'une science thermodynamique, différente, qui est à l'origine de celle que l'on connaît aujourd'hui.
Démonstration
Pour établir ℓ, on observe que le gradient de G(p,T) a un rotationnel nul. Pour établir h, on observe que le gradient de F(V,T) a un rotationnel nul.
Formules de Maxwell
Les formules de Maxwell concernent les dérivées secondes des fonctions d'état, donc les dérivées premières des coefficients calorimétriques.
On obtient ainsi que la dérivée partielle de Cp(p,T) par rapport à p est liée à l'équation d'état. Donc, seule sa valeur à la limite des pressions nulles Cp(0,T) = C0(T) est « libre de choix » : on étudie donc expérimentalement beaucoup cette région de l'espace des états, pour reconstruire une fonction caractéristique du gaz réel.
Il en est de même pour CV(V,T) pour V tendant vers l'infini. On sait déjà par la relation de Mayer que cette limite vaut C0(T) - R.
L'étude expérimentale d'un corps pur gazeux se résume donc à :
- Déterminer l'équation d'état ;
- Déterminer C0(T).
On sait alors reconstruire la fonction d'enthalpie libre G(p,T) qui caractérise toutes les propriétés thermodynamiques du gaz réel.
Autres relations
Il existe en thermomagnétisme des relations similaires (on définit par exemple la désaimantation adiabatique).
Voir aussi
Références
- Portail de la physique
Catégorie : Thermodynamique
Wikimedia Foundation. 2010.