Code de Huffman

Le codage de Huffman est un algorithme de compression qui fut mis au point en 1952 par David Albert Huffman. C'est une compression de type statistique qui grâce à une méthode d'arbre que nous allons détailler plus loin permet de coder les octets revenant le plus fréquemment avec une séquence de bits beaucoup plus courte que d'ordinaire. Cet algorithme offre des taux de compression démontrés les meilleurs possibles pour un codage par symbole (un codage optimal par bit pourrait être obtenu, en théorie du moins, par un codage arithmétique).

Bien qu'optimal, un simple codage de Huffman ne permet pas, en général, d'obtenir les meilleurs ratios de compression. Pour aller plus loin, il faut passer par des méthodes plus complexes réalisant une modélisation probabiliste de la source et tirant profit de cette redondance supplémentaire (Lempel-Ziv, prédiction par reconnaissance partielle, pondération de contextes).

Sommaire 1 Principe 2 Limitations du codage de Huffman 3 Utilisations 4 Anecdote 5 Voir aussi 5.1 Articles connexes 5.2 Liens externes 6 References

Principe

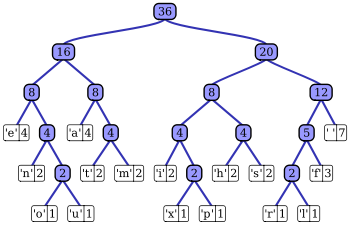
Le principe du codage de Huffman repose sur la création d'un arbre composé de nœuds. Supposons que la phrase à coder est « wikipédia ». On recherche tout d'abord le nombre d'occurrences de chaque caractère (ici les caractères 'a', 'd', 'é', 'k', 'p' et 'w' sont représentés chacun une fois et le caractère 'i' trois fois). Chaque caractère constitue une des feuilles de l'arbre à laquelle on associe un poids valant son nombre d'occurrences. Puis l'arbre est créé suivant un principe simple : on associe à chaque fois les deux nœuds de plus faibles poids pour donner un nœud dont le poids équivaut à la somme des poids de ses fils jusqu'à n'en avoir plus qu'un, la racine. On associe ensuite par exemple le code 0 à la branche de gauche et le code 1 à la branche de droite.

Pour obtenir le code binaire de chaque caractère, on remonte l'arbre à partir de la racine jusqu'aux feuilles en rajoutant à chaque fois au code un 0 ou un 1 selon la branche suivie. Il est en effet nécessaire de partir de la racine pour obtenir les codes binaires car lors de la décompression, partir des feuilles entraînerait une confusion lors du décodage. Ici, pour coder 'Wikipédia', nous obtenons donc en binaire : 101 11 011 11 100 010 001 11 000, soit 24 bits au lieu de 63 (9 caractères x 7 bits par caractère) en utilisant les codes ASCII (7 bits).

Il existe trois variantes de l'algorithme de Huffman, chacune d'elle définissant une méthode pour la création de l'arbre :

1. statique : chaque octet a un code prédéfini par le logiciel. L'arbre n'a pas besoin d'être transmis, mais la compression ne peut s'effectuer que sur un seul type de fichier (ex: un texte en français, où les fréquences d'apparition du 'e' sont énormes; celui-ci aura donc un code très court, rappelant l'alphabet morse).
2. semi-adaptatif : le fichier est d'abord lu, de manière à calculer les occurrences de chaque octet, puis l'arbre est construit à partir des poids de chaque octet. Cet arbre restera le même jusqu'à la fin de la compression. Il sera nécessaire pour la décompression de transmettre l'arbre.
3. adaptatif : c'est la méthode qui offre a priori les meilleurs taux de compression car l'arbre est construit de manière dynamique au fur et à mesure de la compression du flux. Cette méthode représente cependant le gros désavantage de devoir modifier souvent l'arbre, ce qui implique un temps d'exécution plus long. Par contre la compression est toujours optimale et le fichier ne doit pas être connu avant de compresser. Il ne faut donc pas transmettre ou stocker la table des fréquences des symboles. De plus, l'algorithme est capable de travailler sur des flux de données (streaming), car il n'est pas nécessaire de connaitre les symboles à venir.

Limitations du codage de Huffman

On peut montrer que pour une source X, d'entropie H(X) la longueur moyenne L d'un mot de code obtenu par codage de Huffman vérifie:

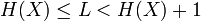
Cette relation, qui montre que le codage de Huffman s'approche effectivement de l'entropie de la source et donc de l'optimum, peut s'avérer en fait assez peu intéressante dans le cas où l'entropie de la source est faible, et où un surcoût de 1 bit devient important. De plus le codage de Huffman impose d'utiliser un nombre entier de bit pour un symbole source, ce qui peut s'avérer peu efficace.

Une solution à ce problème est de travailler sur des blocs de n symboles. On montre alors qu' on peut s'approcher de façon plus fine de l'entropie:

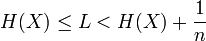
mais le processus d'estimation des probabilités devient plus complexe et coûteux.

De plus, le codage de Huffman n'est pas adapté dans le cas d'une source dont les propriétés statistiques évoluent au cours du temps, puisque les probabilités des symboles sont alors erronées. La solution consistant à ré-estimer à chaque itération les probabilités symboles est impraticable du fait de sa complexité. La technique devient alors le codage Huffman adaptatif : à chaque nouveau symbole la table des fréquences est remise à jour et l'arbre de codage modifié si nécessaire. Le décompresseur faisant de même pour les mêmes causes ... il reste synchronisé sur ce qu'avait fait le compresseur.

En pratique, lorsque l'on veut s'approcher de l'entropie, on préfèrera un codage arithmétique qui est optimal au niveau du bit.

Utilisations

Le codage de Huffman ne se base que sur la fréquence relative des symboles d'entrée (suites de bits) sans distinction pour leur provenance (images, vidéos, sons, etc.). C'est pourquoi il est en général utilisé au second étage de compression, une fois la redondance propre au média mise en évidence par d'autres algorithmes. On pense en particulier à la compression JPEG pour les images, MPEG pour les vidéos et MP3 pour le son, qui peuvent retirer les éléments superflus imperceptibles pour les humains. On parle alors de compression avec perte.

D'autres algorithmes de compression, dits sans perte, tels que ceux utilisés pour la compression de fichiers, utilisent également Huffman pour comprimer le dictionnaire résultant. Par exemple, LZH (Lha) et deflate (ZIP, gzip) combinent un algorithme de compression par dictionnaire (dit de Lempel-Ziv) et un codage entropique de Huffman.

Anecdote

Les premiers Macintosh de la société Apple utilisaient un code inspiré de Huffman pour la représentation des textes : les 15 caractères les plus fréquents d'une langue étaient codés sur 4 bits, et la 16ème configuration servait de préfixe au codage des autres sur un octet (ce qui faisait donc tantôt 4 bits, tantôt 12 bits par caractère). Cette méthode simple se révélait économiser 30% d'espace sur un texte moyen, à une époque où la mémoire vive restait encore un composant coûteux.

Voir aussi

Articles connexes

• Compression de données
• Codage de Shannon-Fano
• Codage arithmétique
• (en) Codage de Shannon-Fano
• (de) Codage de Shannon-Fano et comparaison avec celui de Huffman

Liens externes

• (fr) Codage de Shannon-Fano
• (en) Une implémentation du codage de Huffman en C

References

• D.A. Huffman, "A method for the construction of minimum-redundancy codes" (PDF), Proceedings of the I.R.E., septembre 1952, pp 1098-1102

• Portail de l’informatique