Coalgebre

Coalgebre

Coalgèbre

En mathématiques, la notion de coalgèbre est une notion duale de celle d'algèbre sur un anneau ou sur un corps. Informellement, une algèbre A est un espace vectoriel (ou un R-module) qui est muni en plus d'une multiplication, c'est-à-dire d'une application qui compose deux éléments de A pour en construire un troisième. Une coalgèbre C est donc un espace vectoriel (ou un R-module) muni d'une comultiplication, c'est-à dire-d'une application qui prend un élément de C et qui en retourne deux.

Sommaire

Définition formelle

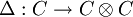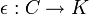Soit K un corps. Une coalgèbre C sur K est un K-espace vectoriel muni de deux applications K-linéaires \Delta : C \to C \otimes C et \epsilon : C \to K telles que :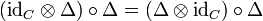

  1. (\mathrm{id}_C \otimes \Delta) \circ \Delta = (\Delta \otimes \mathrm{id}_C) \circ \Delta
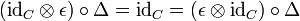  2. (\mathrm{id}_C \otimes \epsilon) \circ \Delta = \mathrm{id}_C = (\epsilon \otimes \mathrm{id}_C) \circ \Delta.

L'application Δ s'appelle le coproduit, et ε la counité. La première condition s'appelle la coassociativité (notion duale de l'associativité dans les anneaux), et la deuxième est l'analogue de la relation que vérifie l'unité (l'élément neutre de la multiplication) dans un anneau.

Relation avec les algèbres

La notion de coalgèbre est dual de celle d'algèbre, dans le sens où le dual topologique de l'espace vectoriel sous-jacent à une coalgèbre C possède une structure naturelle d'algèbre induite par le coproduit de C.

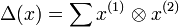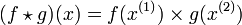En effet, soient f, g deux éléments du dual de C. En posant \Delta(x)=\sum x^{(1)} \otimes x^{(2)} pour tout x de C, on définit le produit de f et de g par : (f \star g)(x) = f(x^{(1)}) \times g(x^{(2)}).

Le fait que Δ soit coassociatif est exactement la condition qui garantit que 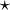\star est associatif.

À l'inverse, si A est une algèbre de dimension finie, alors le dual de A possède une structure naturelle de coalgèbre. En effet, la multiplication de A peut etre vue comme une application 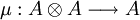\mu:A\otimes A \longrightarrow A. En passant au dual, on obtient une application 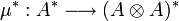\mu^*:A^* \longrightarrow (A\otimes A)^* définie par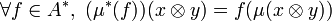

\forall f \in A^*,\ (\mu^*(f))(x \otimes y) = f(\mu(x \otimes y))

Or, si A est de dimension finie, il existe un isomorphisme naturel 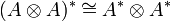(A\otimes A)^* \cong A^*\otimes A^*, donc μ * définit un coproduit, la coassociativité découlant de l'associativité de μ.

Exemple

  • Si E est un K-espace vectoriel de base 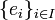\{e_i\}_{i \in I}, alors on définit un coproduit en posant 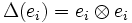\Delta(e_i)=e_i \otimes e_i et en l'étendant linéairement à tout E.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Coalg%C3%A8bre ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coalgebre de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Coalgèbre — En mathématiques, la notion de coalgèbre est une notion duale de celle d algèbre sur un anneau ou sur un corps. Informellement, une algèbre A est un espace vectoriel (ou un R module) qui est muni en plus d une multiplication, c est à dire d une… …   Wikipédia en Français

  • F-coalgèbre — ██████████30  …   Wikipédia en Français

  • Bialgebre — Bialgèbre En mathématiques, une bialgèbre ou bigèbre est un ensemble qui possède à la fois une structure d algèbre et une structure de coalgèbre, et tel que ces deux structures soient compatibles entre elles. Les algèbres de Hopf sont en… …   Wikipédia en Français

  • Bialgèbre — En mathématiques, une bialgèbre ou bigèbre est un ensemble qui possède à la fois une structure d algèbre et une structure de coalgèbre, et tel que ces deux structures soient compatibles entre elles. Les algèbres de Hopf sont en particulier des… …   Wikipédia en Français

  • Cocommutativité — En mathématiques, la cocommutativité est une notion duale de la notion de commutativité. Définition Soit (A,Δ) une coalgèbre. Pour tout x appartenant à A, on note La coalgèbre A est dite cocommutative si  …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Algèbre (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot « algèbre » vient de l arabe ’al ǧabr (« réduction »), désignant une technique de chirurgie des membres puis une technique de… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”