Clef privée

La cryptographie asymétrique, ou cryptographie à clé publique, est une méthode de chiffrement qui s'oppose à la cryptographie symétrique. Elle utilise une clé publique (qui est diffusée) qui permet de coder le message et une clé privée (gardée secrète) qui permet de décoder le message. Ainsi l'expéditeur peut coder le message que seul le destinataire pourra décoder.

Principe

La cryptographie asymétrique, ou cryptographie à clé publique est fondée sur l'existence de fonctions à sens unique — une fois la fonction appliquée à un message, il est extrêmement difficile de retrouver le message original.

En réalité, on utilise en cryptographie asymétrique des fonctions à sens unique et à brèche secrète. Une telle fonction est difficile à inverser, à moins de posséder une information particulière, tenue secrète, nommée clé privée.

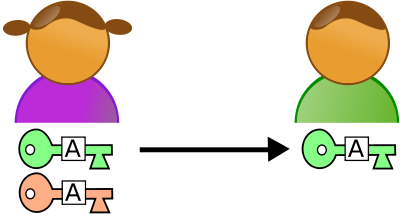
À partir d'une telle fonction, voici comment se déroulent les choses : Alice souhaite pouvoir recevoir des messages chiffrés de n'importe qui. Elle génère alors une valeur à partir d'une fonction à sens unique et à brèche secrète à l'aide d'un algorithme de chiffrement asymétrique (liste ici), par exemple RSA.

Alice diffuse à tout le monde la fonction pour coder les messages (notée clé publique) mais garde secrète la fonction de décodage (notée clé privée).

1^re étape : Alice génère deux clés. La clé publique (verte) qu'elle envoie à Bob et la clé privée (rouge) qu'elle conserve précieusement sans la divulguer à quiconque.

2^e et 3^e étapes : Bob chiffre le message avec la clé publique d'Alice et envoie le texte chiffré. Alice déchiffre le message grâce à sa clé privée.

Chiffrement

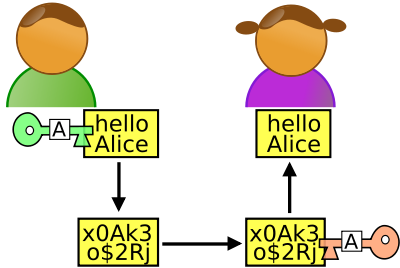
Un des rôles de la clé publique est de permettre le chiffrement ; c'est donc cette clé qu'utilisera Bob pour envoyer des messages chiffrés à Alice. L'autre clé — l'information secrète — sert à déchiffrer. Ainsi, Alice, et elle seule, peut prendre connaissance des messages de Bob, à condition que la brèche ne soit pas trouvée.

Authentification de l'origine

D'autre part, l'utilisation par Alice de sa clé privée sur le condensat d'un message, permettra à Bob de vérifier que le message provient bien d'Alice : il appliquera la clé publique d'Alice au condensat fourni (condensat chiffré avec la clé privée d'Alice) et retrouve donc le condensat original du message. Il lui suffira de comparer le condensat ainsi obtenu et le condensat réel du message pour savoir si Alice est bien l'expéditeur. C'est donc ainsi que Bob sera rassuré sur l'origine du message reçu : il appartient bien à Alice. C'est sur ce mécanisme notamment que fonctionne la signature numérique.

Analogies

Le coffre-fort

Le chiffrement : Alice a choisi un coffre-fort. Elle l'envoie ouvert à Bob, et en garde la clé. Lorsque Bob veut écrire à Alice, il y dépose son message, ferme le coffre, et le renvoie à Alice. À sa réception, seule Alice peut ouvrir le coffre, puisqu'elle seule en possède la clé, à supposer le coffre inviolable, et que personne ne puisse retrouver la clé.

L'authentification ou la signature : Alice place un message dans le coffre-fort qu'elle ferme avec sa clef privée avant de l'envoyer à Bob. Si Bob parvient, à l'aide de la clé publique d'Alice (dont il dispose), à ouvrir le coffre-fort c'est que c'est bien celui d'Alice et donc que c'est bien elle qui y a placé le message.

La boîte à deux serrures

Une autre analogie envisageable serait d'imaginer une boîte avec deux serrures différentes. Lorsque l'on ferme la boîte d'un côté, seule la clé correspondant à l'autre serrure permet l'ouverture de la boîte et vice-versa. Une des clés est privée et conservée secrète, l'autre est dite publique et un exemplaire peut-être obtenu par quiconque souhaite utiliser la boîte.

Pour chiffrer un message Bob prend la boîte, y place son message, et la ferme à l'aide de la clé publique. Seul le détenteur de la clé privée permettant d'accéder à l'autre serrure, Alice en l'occurrence, sera en mesure de rouvrir la boîte.

Pour signer un message, Alice le place dans la boîte et ferme celle-ci à l'aide de sa clé privée. Ainsi n'importe qui ayant récupéré la clé publique pourra ouvrir la boîte. Mais comme la boîte a été fermée par la clé privée, cette personne sera assurée que c'est bien Alice, seule détentrice de cette clé, qui aura placé le message dans la boîte et fermé ladite boîte.

Applications

Transmission sécurisée de la clé symétrique

La cryptographie asymétrique répond à un besoin majeur de la cryptographie symétrique : le partage sécurisé d'une clé entre deux correspondants, afin de prévenir l'interception de cette clé par une personne tierce non autorisée, et donc la lecture des données chiffrées sans autorisation.

Les mécanismes de chiffrement symétrique étant moins coûteux en temps de calcul, ceux-ci sont préférés aux mécanismes de chiffrement asymétrique. Cependant toute utilisation de clé de chiffrement symétrique nécessite que les deux correspondants se partagent cette clé, c'est-à-dire la connaissent avant l'échange. Ceci peut être un problème si la communication de cette clé s'effectue par l'intermédiaire d'un medium non sécurisé, « en clair ». Afin de pallier cet inconvénient, on utilise un mécanisme de chiffrement asymétrique pour la seule phase d'échange de la clé symétrique, et l'on utilise cette dernière pour tout le reste de l'échange.

Mécanismes d'authentification

Un inconvénient majeur de l'utilisation des mécanismes de chiffrement asymétriques est le fait que la clé publique est distribuée à toutes les personnes : Bob, Carole, … souhaitant échanger des données de façon confidentielle. De ce fait, lorsque la personne possédant la clé privée, Alice, déchiffre les données chiffrées, elle n'a aucun moyen de vérifier avec certitude la provenance de ces données (Bob, ou Carole …) : on parle de problèmes d'authentification. Afin de résoudre ce problème, on utilise des mécanismes d'authentification permettant de garantir la provenance des informations chiffrées. Ces mécanismes sont eux aussi fondés sur le chiffrement asymétrique.

Principe d'authentification par chiffrement asymétrique :

Objectif : Bob souhaite envoyer des données chiffrées à Alice en lui garantissant qu'il en est l'expéditeur.

1. Bob crée une paire de clés asymétriques : il conserve la clé privée et diffuse librement la clé publique (notamment à Alice)
2. Alice crée une paire de clés asymétriques : clé privée (qu'elle conserve), clé publique (qu'elle diffuse librement, notamment à Bob)
3. Bob effectue un condensat de son message « en clair » puis chiffre ce condensat avec sa propre clé privée
4. Bob chiffre son message avec la clé publique d'Alice.
5. Bob envoie le message chiffré accompagné du condensat chiffré.
6. Alice reçoit le message chiffré de Bob, accompagné du condensat.
7. Alice déchiffre le message avec sa propre clé privée. À ce stade le message est lisible mais elle ne peut pas être sûre que Bob en est l'expéditeur.
8. Alice déchiffre le condensat avec la clé publique de Bob. A ce stade elle est sûre que le condensat viens de Bob.
9. Alice utilise la même fonction de hachage sur le texte en clair et compare avec le condensat déchiffré de Bob. Si les deux condensats correspondent, alors Alice peut avoir la certitude que Bob est l'expéditeur. Dans le cas contraire, on peut présumer qu'une personne malveillante a tenté d'envoyer un message à Alice en se faisant passer pour Bob !

Cette méthode d'authentification utilise la spécificité des paires de clés asymétriques : si l'on chiffre un message en utilisant la clé publique, alors on peut déchiffrer le message en utilisant la clé privée ; l'inverse est aussi possible : si l'on chiffre en utilisant la clé privée alors on peut déchiffrer en utilisant la clé publique.

Certificats

La cryptographie asymétrique est également utilisée avec les certificats numériques, celui-ci contenant la clé publique de l'entité associée au certificat. La clé privée est quant à elle stockée au niveau de cette dernière entité. Une application des certificats est par exemple la mise en œuvre d'une infrastructure à clés publiques (PKI) pour gérer l'authentification et la signature numérique d'une entité, par exemple un serveur web (Apache avec le module SSL par exemple), ou simplement un client souhaitant signer et chiffrer des informations à l'aide de son certificat de la façon décrite dans les sections précédentes.

Une clé privée inviolable ?

Un chiffrement symétrique au moyen d'une clé de 128 bit propose 2¹²⁸ (un nombre à trente-huit chiffres) façons de chiffrer un message. Un pirate qui essaierait de déchiffrer le message par la force brute devrait les essayer une par une.

Pour les systèmes à clé publique, il en va autrement. Tout d'abord les clés sont plus longues (par exemple 1 024 bit minimum pour RSA) ; ceci est dû au fait qu'elles possèdent une structure mathématique très particulière (on ne peut pas choisir une suite de bits aléatoire comme clé secrète, car, dans le cas du RSA, seuls les nombres premiers sont utilisés). Ensuite, il y a clairement mieux à faire qu'une recherche exhaustive sur, par exemple, 1 024 bit, à savoir exploiter la structure mathématique de la clé (pour RSA, cela mène à la factorisation).

Il faut noter le développement actuel de la cryptographie utilisant les courbes elliptiques, qui permettent (au prix d'une théorie et d'implémentations plus complexes) l'utilisation de clés nettement plus petites que celles des algorithmes classiques (une taille de 160 bit étant considérée comme très sûre actuellement), pour un niveau de sécurité équivalent.

Historique

Le concept de cryptographie à clé publique — autre nom de la cryptographie asymétrique — est dû à Whitfield Diffie et à Martin Hellman. Il fut présenté pour la première fois à la National Computer Conference en 1976, puis publié quelques mois plus tard dans New Directions in Cryptography.

En réalité^[1], James Ellis, qui travaillait au service du chiffre britannique (GCHQ, Government Communications Headquarters), avait eu cette idée peu avant. En 1973, C.C. Cocks décrivit (pour le même service du chiffre) ce qu'on a appelé l'algorithme RSA. Enfin, en 1974, M. J. Williamson invente un protocole d'échange de clé très proche de celui de Diffie et de Hellman. Ces découvertes n'ont été rendues publiques qu'en 1997 par le GCHQ.

Dans leur article de 1976, W. Diffie et M. Hellman n'avaient pas pu donner l'exemple d'un système à clé publique, n'en ayant pas trouvé. Il fallut attendre 1978 pour avoir un premier exemple, dans l'article A Method for Obtaining Digital Signatures and Public-key Cryptosystems de Ronald Rivest, Adi Shamir et Leonard Adleman, le RSA, abréviation tirée des trois noms de ses auteurs. C'est du moins la version académique. Les trois hommes fondèrent aussi la société RSA Security.

Références

Voir aussi

• Cryptographie hybride
• Infrastructures à Clés Publiques (PKI)
• Authentification
• Authentification forte
• Alice et Bob
• Signature numérique
• Chiffrement
• Liste d’algorithmes de cryptographie asymétrique
  • RSA, le plus utilisé d'entre eux
  • Cryptosystème de ElGamal
  • Cryptosystème de Merkle-Hellman

Logiciels de cryptographie asymétrique

• Pretty Good Privacy ou PGP, logiciel existant en versions payante et gratuite (aux fonctionnalités plus réduites).
• GNU Privacy Guard ou GPG ou GnuPG, version libre et gratuite de PGP, qui peut nettement égaler PGP.
• cGeep Pro, implémentation commerciale française d'OpenPGP.
• OpenSSL, version libre et gratuite permettant, notamment, de développer des fonctionnalités à base de chiffrage asymétrique.
• Acid Cryptofiler, version gratuite du logiciel de chiffrement gouvernemental du ministère de la défense français permettant notamment le chiffrement de fichier et de conteneurs montables en disques logiques à base de chiffrement asymétrique.

• Portail de la cryptologie