Cladistique

 Ne doit pas être confondu avec Cladistia.

La cladistique (du grec ancien κλάδος, klados, signifiant « branche »), aussi appelée systématique phylogénétique, est une théorie de classification phylogénétique. Précisément, la cladistique est l'étude de la classification des êtres vivants, selon leurs relations de parenté, dans un cadre évolutionniste. Elle repose sur la construction de groupes monophylétiques dits clades qui incluent un ancêtre commun et l'ensemble de sa descendance.

Exemples de cladogrammes

Description générale

Willi Hennig (1972)

La cladistique se distingue des autres domaines de la systématique car elle cherche à établir les relations de parenté strictes entre les taxons en distinguant caractères dérivés (apomorphies) et primitifs (plésiomorphies). Un groupe monophylétique ne se fondera que sur le partage de caractères dérivés propres, également appelés synapomorphies.

Cette méthode de reconstruction phylogénétique a été introduite dans les années 1950 par l'entomologiste allemand Willi Hennig.

Les résultats de ce type de reconstruction peuvent être représentés sous forme de graphes connexes non cycliques, ou arbres, appelés ici cladogrammes. Ces arbres récapitulent ainsi les relations de parenté entre les taxons considérés. Les données morphologiques, moléculaires et comportementales sont utilisées dans les travaux cladistiques. La reconstruction d'arbres est largement assistée par des logiciels informatiques.

Concepts importants de la cladistique

Le clade comme unité de classification

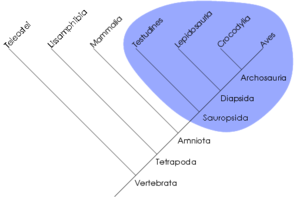
Dans cet arbre phylogénétique, le groupe des sauropsides est monophylétique.

La cladistique reconnait une unité de classement bien particulière, le clade. Un clade est un groupe de taxons formant un groupe monophylétique, une totalité de descendance, un ancêtre commun et tous ses descendants. Ce concept s'oppose à celui du grade, rapprochement de taxons reposant sur d'autres critères (e.g. ressemblance générale, somme de modifications adaptatives). La cladistique qualifiera souvent ces grades de paraphylétiques ou polyphylétiques selon que le rapprochement soit effectué sur la base de plésiomorphies ou d'homoplasies. Certains grades sont cependant monophylétiques. Par exemple, les algues forment un grade polyphylétique, les reptiles forment un grade paraphylétique et les mammifères forment un grade monophylétique.

La notion de clade peut aussi être définie par un ensemble de taxons plus proches qu'ils ne le sont entre eux que de tout autre taxon. Par exemple, les reptiles ne forment pas un clade car certains sont plus apparentés aux oiseaux qu'aux autres reptiles (les Crocodiliens sont inclus dans les Archosauriens comme les oiseaux). Il est à noter qu'un clade représente uniquement une unité évolutive. On parle aussi parfois de groupe holophylétique, ce qui est synonyme de groupe monophylétique.

Paraphylie

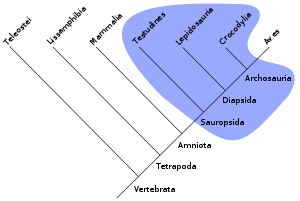
Le groupe paraphylétique des reptiles apparaît en bleu.

Si on parle de groupe monophylétique pour une totalité de descendance, la notion de paraphylie s'applique à un groupe défini sur un ou des caractères plésiomorphes. Ce n'est donc pas une totalité de descendance puisque les organismes portant les états dérivés en sont exclus. Un groupe paraphylétique n'est donc pas monophylétique. Il est donc important en cladistique de bien séparer caractère plésiomorphe et apomorphe pour déterminer si un groupe est monophylétique ou non. La méthode cladistique ne permet donc pas l'existence de groupes tel que les reptiles, les poissons, les invertébrés, les procaryotes, etc. Dans un groupe paraphylétique, certains taxons sont plus proches d'autres taxons hors du groupe que de taxons au sein du groupe paraphylétique. Dans l'exemple des poissons, si on considère les Tétrapodes comme groupe dérivé et les poissons comme groupe primitif par rapport aux Tétrapodes, on constate que certains poissons sont plus proches des Tétrapodes qu'ils ne le sont d'autres poissons : par exemple le Cœlacanthe est plus proche des Tétrapodes que du requin.

La notion de polarisation et de sens de transformation est ici importante. Un caractère pouvant exister sous deux états: primitif (plésiomorphe) ou dérivé (apomorphe), il faut pouvoir déterminer quel état est apomorphe et lequel est plésiomorphe. Pour cela on peut utiliser plusieurs critères dont le plus utilisé est celui du groupe externe. D'autres critères sont utilisés comme le critère ontogénétique et à moindre mesure les critères paléontologique et chorologique. Soient deux états a et b d'un même caractère ; on ne connait pas le sens de transformation entre a et b on a donc a↔b. On peut donc admettre deux sens de transformation : a→b ou b→a. Dans le cas a→b, a se transforme en b, donc a est plésiomorphe par rapport à b et seul b nous renseigne sur les relations de parenté. Dans le cas b→a, b se transforme en a, b est donc plésiomorphe par rapport à a et seul a nous renseigne sur les relations de parenté.

En cladistique un ensemble d'espèces ne peut pas être primitif : il n'y a pas de groupe ancestral. Si un clade contient plusieurs groupes, c'est que chacun de ces groupes a des caractères dérivés qui les distinguent des autres (autapomorphies), ce qui implique qu'un groupe ancestral ne peut pas exister en cladistique. La notion d'ancêtre pourrait s'appliquer à l'espèce, cependant une espèce ancestrale est nécessairement définie par des caractères primitifs donc plésiomorphes par rapport à ses descendants, elle est donc forcément paraphylétique. En cladistique l'ancêtre est donc une hypothèse et n'est pas identifié, ce qui, évidemment, n'implique pas qu'il n'existe pas mais simplement qu'il ne peut pas être défini en tant que taxon ou espèce mais simplement en tant qu'hypothèse d'un ensemble de caractères primitifs (on parle alors de morphotype ancestral).

Homologie vs homoplasie

Le groupe des « animaux à sang chaud » est polyphylétique.

On distingue deux types de ressemblances, l'homologie et l'homoplasie. Des caractères homologues sont hérités d'un ancêtre commun, la relation liant deux homologues étant appelée homologie. À l'inverse, l'homoplasie, terme introduit par Lankester en 1870, caractérise des ressemblances entre caractères n'étant pas hérités d'un ancêtre commun. Différencier l'homoplasie de l'homologie est une tâche compliquée et plusieurs critères définissent l'homologie dont le plus utilisé est le principe des connexions d'Étienne Geoffroy Saint-Hilaire appelé aussi identité des connexions. Ce principe sera repris par Richard Owen. d'après ce principe, sont homologues deux organes si quelles que soient leurs formes ou fonctions, ils ont les mêmes connexions avec d'autres organes. Ce principe peut aisément s'étendre aux séquences moléculaires et l'alignement de séquences correspond à l'application de ce principe.

En réalité ce principe ne permet que de formuler des hypothèses dites d'homologie primaire. En effet rien ne nous assure que le caractère supposé homologue l'est effectivement et que ce n'est pas de l'homoplasie tant que l'hypothèse d'homologie n'est pas testée. Le test effectué est le test de congruence selon Hennig ou de parcimonie. En cladistique on cherche à minimiser le nombre d'hypothèses surnuméraires ou ad hoc. Une hypothèse ad hoc en reconstruction phylogénétique étant l'apparition indépendante d'un caractère dans deux lignées différentes, c'est-à-dire de l'homoplasie. À l'inverse, l'hypothèse de base est que le même caractère observé chez deux taxons indique une relation de parenté. En maximisant alors l'homologie (ou en minimisant l'homoplasie, ce qui constitue deux démarches équivalentes), on obtiendra un test des hypothèses primaires d'homologie. On retiendra alors le cladogramme maximisant l'homologie. Les caractères apparaissant une fois dans le cladogramme résultant de l'analyse de parcimonie seront considérés comme effectivement homologues et donc hérités d'un ancêtre commun. L'homologie secondaire n'est donc plus seulement une homologie déduite du principe des connexions mais une homologie de parenté ou de descendance.

À l'inverse, certains caractères peuvent se révéler homoplastiques une fois l'arbre reconstitué. Ces caractères impliquent au moins deux pas évolutifs ou deux hypothèses de transformation dans le cladogramme résultant. L'homoplasie est donc une hypothèse d'homologie primaire rejetée. Il existe en fait deux types d'homoplasie: la Convergence évolutive et la réversion, décelables entre elles seulement sur l'arbre enraciné le plus parcimonieux. La convergence indique que le même caractère (au sens des connexions et non au sens évolutif) est apparu au moins deux fois dans le groupe considéré. À l'inverse, la réversion est la perte secondaire d'un caractère, c'est-à-dire le retour à l'état primitif. Par exemple l'état primitif des membres pairs chez les Vertébrés est l'absence. L'état dérivé chez les Gnathostomes est leur présence. Or ce caractère est perdu chez les Gymnophiones ou les Serpents. Une réversion est une homoplasie qui s'effectue sur une même morphocline (suite de transformations) alors que la convergence s'effectue sur plusieurs morphoclines distinctes. L'homoplasie n'étant pas un caractère hérité par un ancêtre commun, elle ne nous renseigne pas sur les relations de parenté. Un groupe formé sur une homoplasie est appelé groupe polyphylétique.

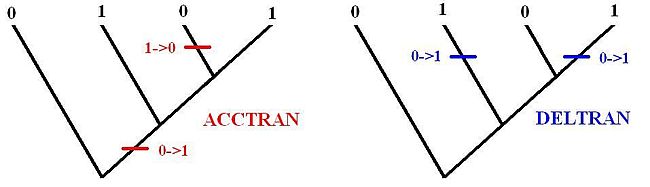
Dans certains cas il n'y a aucun élément pour savoir si l'homoplasie est une réversion ou une convergence, on parle alors de synapomorphie ambigüe^[1]. À partir du cladogramme, le choix de savoir si le caractère est issu d'une convergence ou d'une réversion est arbitraire^[2]. L'hypothèse ACCTRAN (Accelerated transformation) suppose des réversions. L'hypothèse DELTRAN (Delayed transformation) suppose des convergences. Si le choix de l'un ou l'autre n'est pas important en moléculaire, le choix est bien moins anodin pour les phylogénies morphologiques car le choix de l'une ou l'autre des hypothèses change l'interprétation des caractères. Cependant le choix de l'un ou l'autre n'influence pas les relations de parentés. L'image ci dessous l'illustre pour deux arbres ayant la même répartition des caractères, on a deux configurations des transformations différentes.

Illustration d'une synapomorphie ambigüe.

Lecture d'un cladogramme

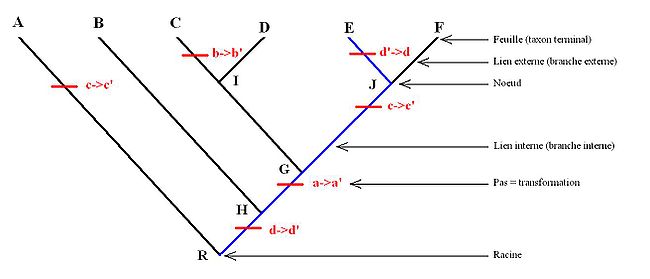
En général les possessions de caractères sont résumées dans un tableau appelé matrice taxons/caractères donnant pour chaque caractère de chaque taxon son état. Ici nous allons utiliser un exemple hypothétique. Par convention, pour chaque caractère "x", l'état primitif est noté x et l'état dérivé x' (ça aurait pu être l'inverse). Tous les caractères en x sont donc plésiomorphes (exemple b) et les caractères en x' son apomorphes (exemple b'). Voici la matrice hypothétique:

On considère l'arbre suivant pour les taxons A, B, C, D, E et F: (A(B((C, D)(E, F)))). Cet arbre est choisi arbitrairement. Ici R=A+B+C+D+E+F: c'est la racine ou le nœud qui contient tout. H=B+C+D+E+F G=C+D+E+F I=C+D et J=E+F, donc G=I+J. Les taxons H, G, I et J sont des nœuds internes (Ce sont des taxons au même titre qu'A, B, C etc.). L'ordre dans lequel les taxons sont disposés ne change pas la lecture de l'arbre. En effet l'arbre (A(B((C, D)(E, F)))) est équivalent à l'arbre ((B((D, C)(E, F)))A)par exemple.

La position la plus parcimonieuse des caractères (en minimisant le nombre de fois où ils apparaissent) est représentée dans l'image associée par des barres rouges où x→x' indique le passage de l'état x à x' et x'→x le passage de l'état x' à l'état x. Les barres rouges représentent des transformations sur l'arbre ou "pas évolutifs".

Exemple de cladogramme.

Selon la disposition la plus parcimonieuse des caractères, le caractère a' est commun à C, D, E, et F, c'est donc une synapomorphie de G.

Le caractère b' n'apparaît que pour un seul taxon terminal : C. C'est donc une autapomorphie de C, c'est-à-dire un caractère dérivé du taxon C uniquement, qui ne nous renseigne pas sur ses relations de parentés avec les autres taxons.

Le caractère "e" reste à l'état e pour tous les taxons, c'est donc une symplésiomorphie de R. Les caractères "c" et "d" subissent deux transformations (deux pas) dans l'arbre, ce sont donc des homoplasies.

Sur la ligne bleue (allant de la racine à E), le caractère "d" est impliqué deux fois sous l'état de caractère d, c'est donc une réversion. Pour le caractère "d" on a alors la morphocline, ou suite de transformations suivante : d→d'→d. L'état de caractère d possédé par E n'est donc pas réellement primitif mais semblable à l'état primitif.

Le caractère "c" apparaît dans deux morphoclines différentes sous l'état c', c'est donc une convergence. Les deux états de "c" pour A et J ne sont donc pas des homologies secondaires : ce n'est pas le même caractère hérité d'un ancêtre commun.

Sur cet arbre on peut compter le nombre de transformations, il y en a 6. On compte donc 6 pas.

Deux groupes frères sont les groupes les plus apparentés entre eux qu'ils ne le sont de n'importe quel autre. Ici par exemple C est groupe frère de D, B groupe frère de G, J groupe frère de I, etc.

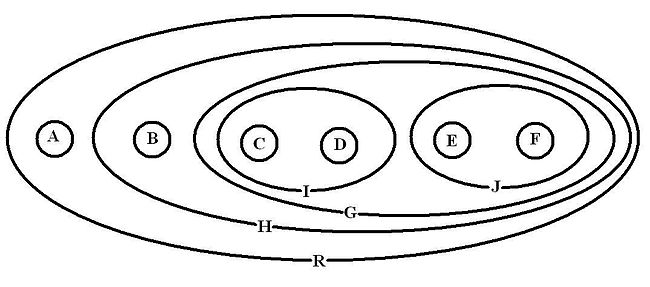
Un cladogramme représente une hiérarchie, au sens mathématique du terme, c'est-à-dire un ensemble de classes strictement incluses les unes dans les autres. En effet, ici C et D appartiennent à I et tous les groupes appartiennent à R (R étant la racine donc la classe comprenant tout). Un cladogramme peut donc être représenté en diagramme de Venn. L'image ci-dessous représente le cladogramme utilisé dans l'exemple sous forme de diagramme de Venn.

Cladogramme précédent sous forme de diagramme de Venn illustrant la structure hiérarchique des relations entre taxons

Enracinement et groupe externe

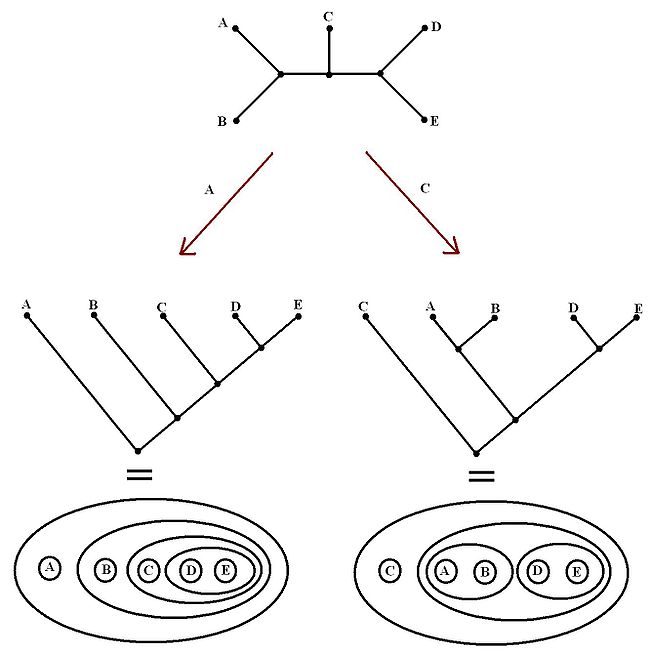
La principale manière de polariser un caractère qui est utilisée est l'utilisation d'un groupe externe ou extra-groupe (outgroup)^[3]. On estime que tout état de caractère présent en dehors du groupe interne (ou in-group) est antérieur au groupe interne car déjà présent ailleurs. On va donc considérer ce caractère comme primitif. Tout état de caractère présent en dehors du groupe d'étude est donc considéré comme primitif et tout état qui n'est présent que dans le groupe d'étude est considéré comme dérivé, car propre au groupe d'étude. Au lieu d'utiliser cette procédure pour chaque caractère, on utilise un groupe entier en considérant tous ces caractères. Ce groupe doit être considéré a priori comme externe du groupe d'étude. Par exemple pour une phylogénie des tétrapodes on pourra utiliser un téléostéen ou pour une phylogénie des gastéropodes on pourra utiliser un céphalopode ou un bivalve. Le groupe externe ne doit pas être trop éloigné du groupe d'étude sinon les caractères ne pourront même pas être comparés. A l'inverse, s'il est trop proche le groupe externe peut en fait faire partie du groupe interne. De plus, si certains états de caractères du groupe externe sont homoplastiques avec ceux du groupe interne, la polarisation de certains caractères peut être fausse. Par exemple si on polarise une phylogénie des mammifères avec seulement des oiseaux, on peut considérer que l'état de caractère "aile" est primitif pour le membre antérieur des mammifères, ce qui est bien évidemment faux. Le bon choix du groupe externe est donc crucial et un mauvais choix peut entraîner des incohérences.

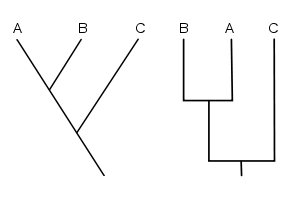
Le groupe externe permet alors d'enraciner l'arbre en l'orientant. Dans l'image ci-dessous, l'arbre de départ n'est pas enraciné alors que les deux arbres d'en dessous (avec soit A, soit C en groupe externe) sont enracinés. Les relations de parenté et le sens des transformations de caractères ne peuvent donc être inférées qu'à partir d'un arbre enraciné. On remarque que la topologie de l'arbre change considérablement selon le groupe externe utilisé. Les représentations en diagramme de Venn (en bas) sont les mêmes que les cladogrammes en forme d'arbres (en haut) respectivement à droite et à gauche. On constate que les structures d'inclusions sont différentes. L'arbre de gauche et de droite peuvent aussi être représentés en parenthétique: (A(B(C(D, E)))) à gauche et (C(A, B)(D, E)) à droite.

L'arbre du haut n'est pas enraciné. L'arbre de gauche est enraciné en prenant A comme groupe externe. L'arbre de droite est enraciné en prenant C comme groupe externe.

Cladistique et évolution

Il est important de bien distinguer deux concepts différents, le "pattern" et le "process". La cladistique permet de comprendre le "Pattern" ou structure de parenté entre les espèces actuelles ou fossiles, c'est-à-dire leurs relations de parentés, tandis que l'évolution répond à la notion de processus évolutif ou "Process", c'est-à-dire comment les caractères des espèces évoluent et sont acquis (ex : la sélection naturelle). Dès lors les cladogrammes représentent uniquement des classifications entre espèces ou taxons. Il est cependant évident que les caractères, qui permettent de faire des clades, sont le résultat de mécanismes évolutifs mais la cladistique ne cherche ni à les expliquer, ni à les connaître. Seuls les liens de parenté sont recherchés en cladistique. Cependant le cladogramme résultant de l'analyse permettra d'interpréter l'évolution des clades et des caractères. En effet, le clade étant une unité évolutive, connaître la structure de parenté de taxon permet d'interpréter la distribution des caractères au cours du temps, et donc l'évolution de ces caractères.

les méthodes cladistiques

Différents méthodes peuvent être appliqués dans le cadre de reconstructions phylogénétiques cladistiques. Le principe de parcimonie, selon lequel l'explication la plus simple (ici l'arbre ayant le moins de pas évolutifs) doit être retenue est très majoritairement utilisée. En phylogénie moléculaire et dans de rares cas en morphologie, une autre méthode très proche de la parcimonie est parfois aussi employée : l'optimisation directe. On compte aussi la méthode de compatibilité (aujourd'hui tombée en désuétude) et l'analyse à trois éléments (three-items analysis, ou 3ia)^[4], très minoritaire aujourd'hui. Hennig lui même n'a jamais utilisé ces méthodes, préférant une méthode d'argumentation. On parle d'argumentation Hennigienne. Cependant aujourd'hui une phylogénie n'est que très rarement acceptée sans analyse algorithmique préalable.

La parcimonie

La philosophie derrière les méthodes de parcimonie se fonde sur un principe attribué à Guillaume d'Ockham, selon lequel les entités ne doivent pas être multipliées par delà ce qui est nécessaire (« Entia non sunt multiplicanda praeter necessitatem »). Pour faire un choix entre deux arbres, l'on va donc considérer que le plus court, i.e. l'arbre avec le moins de pas évolutifs, est l'arbre représentant l'hypothèse phylogénétique la plus plausible. L'on distingue trois modèles de parcimonie, selon la considération des convergences et des réversions :

• La parcimonie de Wagner, où convergences et réversions sont acceptées.
• La parcimonie de Camin-Sokal admet les convergences mais pas les réversions.
• La parcimonie de Dollo accepte les réversions mais pas les convergences.

À titre d'exemple, l'absence de fenêtre antéorbitaire chez les crocodiles actuels est considéré comme une réversion (elle était présente chez leurs ancêtres putatifs) ; les topologies similaires du bassin des oiseaux et des ornitischiens, ou encore les formes hydrodynamiques des delphinidés et de la plupart des lamniformes sont considérées comme des convergences.

L'optimisation directe

Cette méthode ne nécessite pas d'alignement avant l'analyse, celui ci se faire au fur e à mesure de l'analyse de telle manière que l’alignement obtenu après analyse permette l'arbre le plus parcimonieux possible. L'arbre obtenu par optimisation directe est donc théoriquement donc plus parcimonieux qu'un arbre obtenu par une autre méthode d'alignement [1].

La compatibilité

Cette méthode, largement tombée dans l'obsolescence, va qualifier les caractères pour lesquelles il existe un arbre montrant les différents états de caractère sans comporter d'homoplasie de caractères mutuellement compatibles. Dans une analyse phylogénétique, l'ensemble des caractères mutuellement compatibles formera une clique. L'arbre retenu sera construit à partir de la clique la plus importante et sera dépourvu de caractères homoplastiques.

L'analyse à trois éléments

L'analyse à trois éléments ou 3ia (Three item analysis, parfois aussi appelée TTS pour Three-Taxon Statements) est une méthode cladistique qui reconstitue les hypothèses de parentés en décomposant les hypothèses d'homologie en hypothèses minimales d'homologie, c'est-à-dire en sous-arbres minimaux (à trois éléments en cherchant "si un premier taxon est plus proche d'un deuxième que d'un troisième", d'où le nom de la méthode) appelés 3is pour "three item statements" ou assertions à trois éléments. Cette méthode a d'abord été utilisée pour la biogéographie cladistique et a ensuite été utilisée pour l'étude cladistique des taxons. La 3ia part d'hypothèses d'homologies sous forme d'arbres racinés représentant les relations entre caractères homologues qui sont ensuite décomposés en sous arbres, cette méthode ne nécessite donc pas de groupe externe mais demande de connaitre à priori les états dérivés ou primitifs des caractères. On parle aussi parfois d'analyse à trois taxons.

L'argumentation Hennigienne

Cette procédure qui ne passe pas par un algorithme automatisé, consiste à proposer une phylogénie (ou schéma d'argumentation) puis de l'argumenter en fonction de caractères explicitement donnés par l'auteur tout en distinguant les états primitifs et dérivés de ces caractères.

Voir aussi

• Caractère ancestral et caractère dérivé
• Willi Hennig
• Monophylie
• Paraphylie
• Polyphylie
• Synapomorphie
• Autapomorphie
• Analyse à trois éléments

Bibliographie

• P. Tassy, La renaissance de la systématique, 2001 En ligne (fr)
• H. Le Guyader, G. Lecointre, Classification phylogénétique du vivant 3ème édition, Belin, 2001.
• P. Tassy L'arbre à remonter le temps, Christian Bourgois, Paris, 1991.
• P. Darlu & P. Tassy, La reconstruction phylogénétique. Concepts et Méthodes, Masson, 1993 En ligne (fr)
• W. Hennig, Phylogenetic Systematics, Illinois University Press, 1966, traduit par D. Dwight Davis & R. Zangerl.
• I.J. Kitching, P.L. Forey, C.J. Humphries et D.M. Williams, Cladistics, Oxford, Oxford University Press, 1998 (2^e éd.).
• C. Patterson, Morphological characters and homology, in K.A. Joysey et A.E. Friday (éd.), Problems in Phylogenetic Reconstruction, Londres, Academic Press, 1982.
• K. de Queiroz et J.A. Gauthier, « Phylogenetic taxonomy », Annual Review of Ecology and Systematics n^o 23, 1992, p. 449–480.
• D.L. Swofford, G.J. Olsen, P.J. Waddell et D.M. Hillis, Phylogenetic inference, in D.M. Hillis, C. Moritz et B.K. Mable (éd.), Molecular Systematics, Sunderland (Massachusetts), Sinauer Associates, 1996.
• E.O. Wiley, Phylogenetics : The Theory and Practice of Phylogenetic Systematics.-, New York, Wiley Interscience, 1981.

Autres références

Liens externes

• (en) The Willi Hennig Society website

• Portail de la biologie
• Portail de l’origine et de l’évolution du vivant