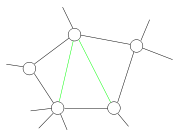
Chordal graph

Un cycle, en noir, avec deux cordes, en vert. Si l'on s'en tient à cette partie, le graphe est cordal. Supprimer l'une des arêtes vertes rendrait le graphe non cordal. En effet, l'autre arête verte formerait, avec les trois arêtes noires, un cycle de longueur 4 sans corde.

En théorie des graphes, on dit qu'un graphe est cordal si chacun de ses cycles de quatre sommets ou plus possède une corde, c'est-à-dire une arête reliant deux sommets non-adjacents du cycle. Une définition équivalente est que tout cycle sans corde possède au plus trois sommets. Les graphes cordaux, aussi appelés graphes triangulés, sont un sous-ensemble des graphes parfaits.

Élimination parfaite et reconnaissance efficace

Un ordonnancement d'élimination parfaite d'un graphe est un ordonnancement des sommets du graphe tel que, pour tout sommet v, l'ensemble formé par v et ses voisins qui se trouvent après lui forment une clique. Un graphe est cordal si et seulement si il possède un ordonnancement d'élimination parfaite. (Fulkerson and Gross 1965).

Rose et al (1976; voir aussi Habib et al 2000) montrent qu'un ordonnancement d'élimination parfaite d'un graphe cordal peut être trouvé de manière efficace en utilisant un algorithme appelée recherche lexicographique en largeur d'abord. Cet algorithme maintient une partition des sommets du graphe sous forme d'une séquence d'ensembles. Au début, cette séquence est un seul ensemble avec tous les sommets. L'algorithme va ensuite choisir de manière répétée un sommet v de l'ensemble le plus jeune dans la séquence qui contient les sommets pas encore choisis, et sépare chaque ensemble S de la séquence en deux sous-ensembles, l'un contenant les voisins de v dans S et l'autre les sommets non-voisins. Quand cette séparation a été faite pour tous les sommets, la séquence est composée d'ensembles ne contenant qu'un seul sommet. Ces sommets se retrouvent dans l'ordre inverse de l'ordonnancement d'élimination parfaite.

Comme la recherche lexicographique en largeur d'abord et le fait de tester si un ordonnancement est un ordonnancement d'élimination parfaite peuvent être effectués en temps linéaire, il est possible de savoir si un graphe est cordal en temps linéaire.

L'ensemble de tous les ordonnancements d'élimination parfaite d'un graphe cordal peut être modélisé comme les mots de base d'un antimatroïde; Chandran et al. (2003) ont utilisés cette connexion avec les antrimatroïdes dans un algorithme listant efficacement tous les ordonnancements d'élimination parfaite d'un graphe cordal donné.

Cliques maximales et coloration de graphes

Une application de l'ordonnancement d'élimination parfaite est la recherche d'une clique maximum d'un graphe cordal en temps polynomial. Le problème similaire, mais pour un graphe quelconque, est NP-complet. De manière générale, le nombre de cliques maximales dans un graphe cordal croît linéairement, tandis que cette croissance peut être exponentielle dans des graphes non cordaux. Pour lister toutes les cliques maximales d'un graphe cordal, il suffit de trouver un ordonnancement d'élimination parfaite, de créer une clique pour chaque sommet v avec les voisins de v venant après v dans l'ordonnancement d'élimination parfaite, et de tester pour chacune des cliques ainsi formées si est maximale.

La plus grande clique maximale est une clique maximum et, comme les graphes cordaux sont des graphes parfaits, la taille de la clique est le nombre chromatique du graphe cordal. Un graphe cordal étant un graphe parfaitement ordonnançable, une coloration optimale peut être obtenue par application d'un algorithme de coloration gloutonne aux sommets dans l'ordre inverse de celui de l'ordonnancement d'élimination parfaite. (Maffray 2003).

Graphes d'intersection de sous-arbres

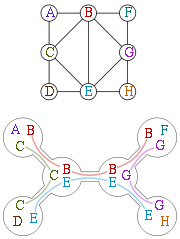Un graphe cordal à huit sommets, représenté comme le graphe d'intersection de huit sous-arbres d'un arbre à six noeuds

Une autre caractérisation des graphes cordaux faite par Gavril (1974), utilise les arbres et leurs sous-arbres.

À partir d'une collection de sous-arbres d'un arbre A, il est possible de définir un graphe sous-arbre qui est un graphe d'intersection avec un sommet par sous-arbre. Les arêtes relient les sous-arbres qui ont au moins un nœud en commun dans l'arbre A. Comme Gavril l'a montré, les graphes sous-arbre sont exactement les graphes cordaux. Cette représentation forme une décomposition arborescente du graphe, où la hauteur du graphe vaut la taille de la plus grande clique du graphe moins un; la décomposition arborescente de n'importe quel graphe G peut être vue de cette manière comme une représentation de G comme un sous-graphe d'un graphe cordal.

Relation avec les autres classes de graphe

Sous-classes

Les graphes d'intervalle sont les graphes d'intersection de sous-arbres de graphes chemin; ainsi, ils sont une sous-famille des graphes cordaux.

Les graphes fendus sont exactement les graphes à la fois cordaux et complémentaires de graphes cordaux. Bender et al. (1985) ont montré, en notant F(n) le nombre de graphes fendus à n sommets et C(n) le nombre de graphes cordaux à n sommets, que F(n) / C(n) tendait vers 1 lorsque n tendait vers l'infini.

Les graphes de quasi-seuil sont exactement les graphes qui sont à la fois cordaux et cographes.

Sur-classes

Les graphes cordaux sont une sous-classe des graphes paires sans trou, car les graphes cordaux peuvent ou contenir un nombre paire de trous ou n'en contenir aucun.

Références

• Bender, E. A.; Richmond, L. B.; Wormald, N. C., « Almost all chordal graphs split », dans J. Austral. Math. Soc., Series A, vol. 38, n^o 2, 1985, p. 214–221 
• Chandran, L. S.; Ibarra, L.; Ruskey, F.; Sawada, J., « Enumerating and characterizing the perfect elimination orderings of a chordal graph », dans Theoretical Computer Science, vol. 307, 2003, p. 303–317 [texte intégral lien DOI] 
• Fulkerson, D. R.; Gross, O. A., « Incidence matrices and interval graphs », dans Pacific J. Math, vol. 15, 1965, p. 835–855 [texte intégral] 
• Gavril, Fănică, « The intersection graphs of subtrees in trees are exactly the chordal graphs », dans Journal of Combinatorial Theory, Series B, vol. 16, 1974, p. 47–56 [lien DOI] 
• Maffray, Frédéric (2003), "On the coloration of perfect graphs", in Reed, Bruce A.; Sales, Cláudia L., Recent Advances in Algorithms and Combinatorics, CMS Books in Mathematics, 11, Springer-Verlag, pp. 65–84, doi:10.1007/0-387-22444-0_3 .
• Rose, D.; Lueker, George; Tarjan, Robert E., « Algorithmic aspects of vertex elimination on graphs », dans SIAM J. Computing, vol. 5, 1976, p. 266–283 [lien DOI] 

Liens externes

• Information System on Graph Class Inclusions: chordal graph

• Portail de l’informatique
• Portail des mathématiques