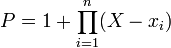Champ Algébriquement Fermé

Champ Algébriquement Fermé

Corps algébriquement clos

En mathématiques, un corps K est dit algébriquement clos si tout polynôme de degré supérieur ou égal à un, à coefficients dans K, admet (au moins) une racine dans K.

Dans ce cas, chacun de ces polynômes se divise en facteurs linéaires. Il peut être démontré qu'un corps est algébriquement clos si et seulement s'il n'a pas d'extension algébrique propre, et ceci est parfois pris comme définition.

Par exemple, le corps des nombres réels n'est pas algébriquement clos, parce que le polynôme X2 + 1 n'a pas de racine réelle. Au contraire, le corps des nombres complexes est algébriquement clos : c'est le théorème fondamental de l'algèbre.

Tout corps a une clôture algébrique, qui est le plus petit corps algébriquement clos dont K est un sous-corps. La clôture algébrique d'un corps donné est unique à K-isomorphisme (isomorphisme laissant invariants les éléments de K) près. En particulier, le corps des nombres complexes est la clôture algébrique du corps des nombres réels et le corps des nombres algébriques est la clôture algébrique du corps des nombres rationnels.

Un corps fini K ne peut être algébriquement clos. En effet, si 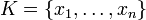K =\{x_1,\dots,x_n\}, le polynôme

P = 1 + \prod_{i = 1}^n (X - x_i)

n'admet aucune racine dans K (il prend la valeur 1 en chaque élément de K).

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Corps alg%C3%A9briquement clos ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Champ Algébriquement Fermé de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Champ algébriquement fermé — Corps algébriquement clos En mathématiques, un corps K est dit algébriquement clos si tout polynôme de degré supérieur ou égal à un, à coefficients dans K, admet (au moins) une racine dans K. Dans ce cas, chacun de ces polynômes se divise en… …   Wikipédia en Français

  • clos — 1. clos, close [ klo, kloz ] adj. • v. 1130; de clore 1 ♦ Fermé. Espace clos. ⇒ 1. enceinte; 2. clos, enclos. Combat singulier, tournoi en champ clos. Volets clos. Loc. Trouver porte close : ne trouver personne. À huis clos. (1931) MAISON CLOSE,… …   Encyclopédie Universelle

  • Arithmétique complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… …   Wikipédia en Français

  • Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… …   Wikipédia en Français

  • Nombre complexe — Pour les articles homonymes, voir complexe. En mathématiques, les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels …   Wikipédia en Français

  • Nombres complexes — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… …   Wikipédia en Français

  • Nombres imaginaires — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… …   Wikipédia en Français

  • Notation complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… …   Wikipédia en Français

  • ℂ — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”