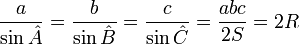Cercle circonscrit a un triangle
- Cercle circonscrit a un triangle
-
Cercle circonscrit à un triangle
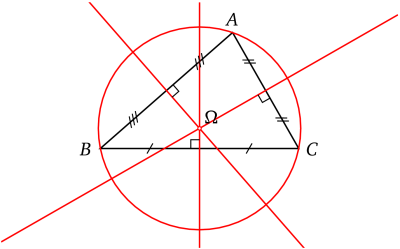
Médiatrices et cercle circonscrit d'un triangle.
En géométrie du triangle, le cercle circonscrit à un triangle est l'unique cercle passant par ses trois sommets.
Le centre de ce cercle est le point de concours des médiatrices des côtés du triangle. Son rayon peut s'exprimer avec la loi des sinus.
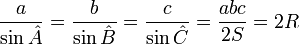
où a, b et c désignent les longueurs des trois côtés du triangle ; 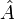 ,
, 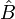 et
et 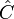 désignent respectivement les angles opposés à chacun des côtés a, b et c ; et S désigne l'aire du triangle.
désignent respectivement les angles opposés à chacun des côtés a, b et c ; et S désigne l'aire du triangle.
Propriétés élémentaires
- Propriété
- Les trois médiatrices d'un triangle sont concourantes en un point
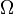 équidistant des trois sommets (qui est aussi le « centre du cercle circonscrit », voir ci-dessous).
équidistant des trois sommets (qui est aussi le « centre du cercle circonscrit », voir ci-dessous).
Démonstration
Notons Ω l'intersection des deux médiatrices des segments [AB] et [AC].
- Ω est sur la médiatrice de [AB] donc AΩ = BΩ.
- Ω est sur la médiatrice de [AC] donc AΩ = CΩ.
Donc CΩ = BΩ : par suite Ω est sur la médiatrice du segment [BC]. Les trois médiatrices sont donc concourantes en Ω.
- Propriété
- Il existe un et un seul cercle passant à la fois par les trois sommets du triangle. Ce cercle de centre
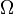 est appelé « cercle circonscrit » au triangle.
est appelé « cercle circonscrit » au triangle.
Démonstration
- Existence
- Elle a été prouvée ci-dessus : AΩ = CΩ = BΩ donc le cercle de centre Ω et passant par A passe aussi par B et C.
- Unicité
- Si un cercle passe à la fois par A et B, son centre appartient à la médiatrice de [AB]. S'il passe par A et C, son centre appartient à la médiatrice de [AC]. Donc, si un cercle passe par les trois points A, B et C, son centre appartient à la fois aux médiatrices de [AB] et de [AC], c'est-à-dire à leur intersection. Celle-ci se réduit à un point, Ω ; le cercle a donc nécessairement pour centre Ω. Le rayon du cercle est donc égal à AΩ. On a unicité du centre et du rayon, donc du cercle.
Propriétés remarquables
Voir aussi
Articles connexes
 Portail de la géométrie
Portail de la géométrie
Catégories : Géométrie du triangle | Cercle et sphère
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Cercle circonscrit a un triangle de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Cercle Circonscrit À Un Triangle — Médiatrices et cercle circonscrit d un triangle. En géométrie du triangle, le cercle circonscrit à un triangle est l unique cercle passant par ses trois sommets. Le centre de ce cercle est le point de concours des médiatrices des côtés du… … Wikipédia en Français
Cercle circonscrit à un triangle — Médiatrices et cercle circonscrit d un triangle. En géométrie du triangle, le cercle circonscrit à un triangle est l unique cercle passant par ses trois sommets. Le centre de ce cercle est le point de concours des médiatrices des côtés du… … Wikipédia en Français
Cercle Circonscrit — Cercles circonscrits à des triangles En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone inscriptible. Les sommets… … Wikipédia en Français
Cercle circonscrit — En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone inscriptible. Les sommets sont alors cocycliques, situés sur un … Wikipédia en Français
Centre Du Cercle Circonscrit — Cercle circonscrit Cercles circonscrits à des triangles En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone… … Wikipédia en Français
Centre du cercle circonscrit — Cercle circonscrit Cercles circonscrits à des triangles En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone… … Wikipédia en Français
Circonscrit (géométrie) — Cercle circonscrit Cercles circonscrits à des triangles En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone… … Wikipédia en Français
Cercle circonscri — Cercle circonscrit Cercles circonscrits à des triangles En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone… … Wikipédia en Français
Triangle isocèle — Triangle Pour les articles homonymes, voir Triangle (homonymie) … Wikipédia en Français
Triangle scalène — Triangle Pour les articles homonymes, voir Triangle (homonymie) … Wikipédia en Français
 Médiatrices et cercle circonscrit d'un triangle.
Médiatrices et cercle circonscrit d'un triangle.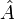 ,
, 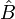 et
et 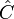 désignent respectivement les angles opposés à chacun des côtés a, b et c ; et S désigne l'aire du triangle.
désignent respectivement les angles opposés à chacun des côtés a, b et c ; et S désigne l'aire du triangle.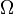 équidistant des trois sommets (qui est aussi le « centre du cercle circonscrit », voir ci-dessous).
équidistant des trois sommets (qui est aussi le « centre du cercle circonscrit », voir ci-dessous).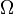 est appelé « cercle circonscrit » au triangle.
est appelé « cercle circonscrit » au triangle.