Cavité optique

Une cavité optique, ou résonateur optique est un dispositif dans lequel certains rayons lumineux sont susceptible de rester confinés grâce à des miroirs sur lesquels ils se réfléchissent. Ces cavités sont indispensables aux lasers pour que leur lumière passe plusieurs fois dans leur milieu amplificateur. Elles sont parfois présentes dans des interféromètres et des oscillateurs paramétriques optiques.

Types de cavité

Différentes cavités à deux miroirs :
1. plane.
2. concentrique.
3. hémisphérique.
4. confocale.
5. concave-convexe.

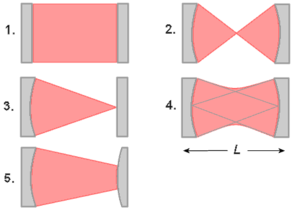
La façon la plus simple de réaliser une cavité optique est de placer deux miroirs plans ou sphériques face-à-face séparés d'une distance L. On retrouve cette configuration dans l'interféromètre de Fabry-Pérot, ainsi que dans de nombreux lasers de petite taille. Malgré sa simplicité, cette disposition est inutilisable dans le matériel de grande taille à cause de la difficulté d'alignement : les miroirs doivent être parallèles à quelques secondes d'arc près afin que la lumière ne s'échappe pas trop vite. Ce problème est plus facile à résoudre lorsque la cavité est de petite taille. On les retrouve ainsi dans les microcavités optiques et les lasers à semi-conducteurs.

Avec deux miroirs sphériques de rayons de courbure R₁ et R₂, de nombreuses configurations de cavités peuvent être réalisées. Si les deux miroirs ont le même centre (R₁ + R₂ = L), cela forme une cavité concentrique. En remplaçant un des deux miroirs par un miroir plan placé au centre de l'autre, on obtient une cavité hémisphérique.

Une configuration importante et souvent utilisée est la cavité confocale, où les deux miroirs sont identiques et dont les rayons de courbure coïncident avec la longueur de la cavité (R₁ = R₂ = L). Ce type de cavité permet de produire des faisceaux les plus fins possibles.

Il existe aussi des cavités concave-convexes constituées de deux miroirs sphériques : un concave et un convexe. Cela permet de ne pas trop focaliser le faisceau, ce qui est parfois important dans les lasers de grande puissance pour ne pas détruire le milieu amplificateur.

Modes de résonance

La lumière réfléchie plusieurs fois par les miroirs peut interférer avec elle-même. Il en découle que seules quelques longueurs d'onde, et leurs ondes associées, peuvent être présentes dans la cavité. Ces ondes sont appelées les modes de résonance. Ils dépendent de la forme de la cavité.

On définit deux types de modes : les modes longitudinaux qui diffèrent par leur longueur d'onde, et les modes transverses qui diffèrent en plus par leur forme. Dans le cas général, on peut observer une superposition de ces modes.

Il existe aussi des cavités dans lesquelles toutes les longueurs d'onde sont possibles. Dans ce cas on ne définit pas de modes de résonance.

Stabilité

Une cavité constituée de deux miroirs ne peut confiner la lumière que dans certaines positions des miroirs. Dans ces cas, on dit que la cavité est stable. Si elle est instable, un rayon présent dans la cavité en sortira après quelques réflexions sur les miroirs, et sera perdu. Il est possible de calculer la condition de stabilité de telles cavités :

.

Les cavités vérifiant ce critère sont stables.

Les cavités en pratique

Si une cavité optique n'est pas vide (une cavité laser, par exemple, contient un milieu amplificateur), la valeur de L utilisée n'est pas la vraie distance séparant les miroirs, mais la longueur effective de la cavité obtenue avec l'optique matricielle (à ne pas confondre avec le chemin optique). De même, les lentilles présentes dans la cavité ainsi que les effets des inhomogénéités des milieux amplificateurs modifient les modes de résonance et la stabilité.

Les cavités utilisées dans les lasers peuvent contenir plus de deux miroirs, ainsi que d'autres éléments permettant de modifier le faisceau, comme des modulateurs acousto-optique, des filtres spatiaux, des fibres optiques, des prismes et des réseaux optiques.

La configuration choisie doit également tenir compte des aberrations optiques et des réflexions à l'angle de Brewster.

Lien externe

• Consortium "Optique Pour l'Instrumentation", FORGET, S, cours en ligne, 2008, "Optique des Lasers et Faisceaux Gaussiens" <http://prn1.univ-lemans.fr/prn1/siteheberge/optique/M1G3_SForget/co/M1G3_web.html>

• Portail de la physique